A body is released from the top of an inclined plane of inclination theta. It reaches the bottom with velocity V. If keeping the length same the angle of the inclination is doubled what will be the velocity of the body and reaching the ground?
1 Answer
Explanation:
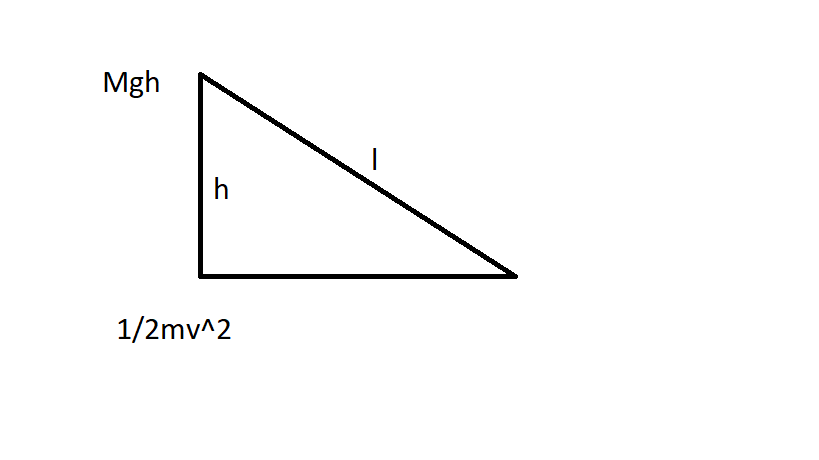
let the height of incline be initially be
The figure show Energy diagram at the different points of the inclined plane.
there for
and the
but ,now after change new angle is (
Let
[since length of the inclined has not yet changed.]
using (i) and (ii)
we get the new height as ,
by conserving the Total mechanical energy,
we get,
putting
or (to reduce variables)
but the initial velocity is
or
Hence ,the velocity becomes

