A company can sell 5000 chocolate bars a month at $0.50 each. If they raise the price to $0.70, sales drop to 4000 bars per month. The company has fixed costs of $1000 per month and $0.25 for manufacturing each bar. What price will maximize the profit?
1 Answer
Profit maximising price is
Explanation:
Let us first arrive at demand function.
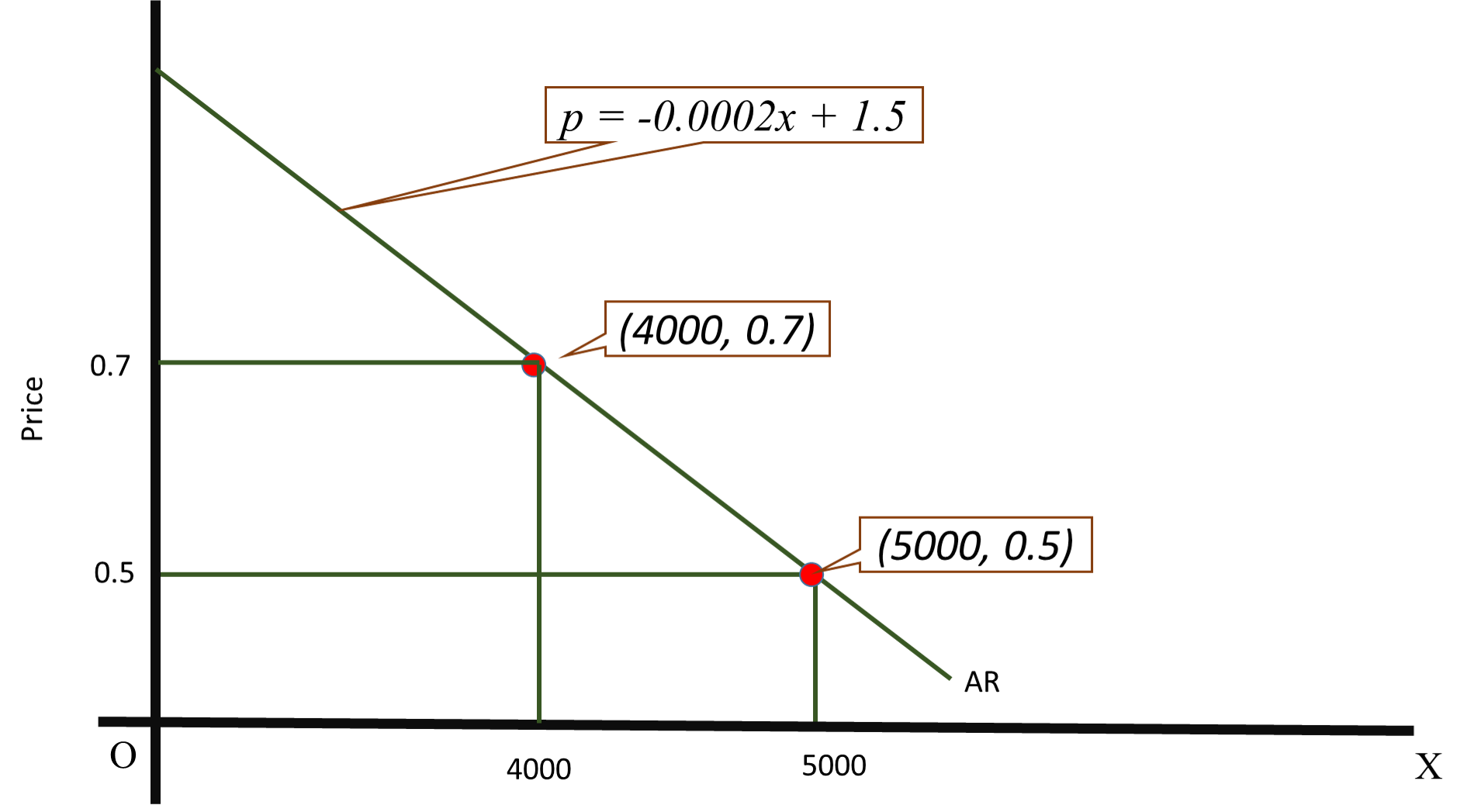
Look at the graph. When the price is $0.5, the seller sells 5000 bars. When the price goes up to $0.7, the seller can sell only 400 bars.
From this information, we have to deduce the demand curve.
It is a linear demand curve. use the straight line formula to arrive at demand function.
#p-p_1=(p_2-p_1)/(x_2-x_1)(x-x_1)#
Where -
#x_1=5000#
#p_1=0.5#
#x_2=4000#
#p_2=0.7#
Substitute these values in the above formula
#p-0.5=(0.7-0.5)/(4000-5000)(x-5000)#
#p-0.5=(0.2)/(-1000)(x-5000)#
#p-0.5=-0.0002(x-5000)#
#p-0.5=-0.0002x+1#
#p=-0.0002x+1+0.5#
#p=-0.0002x+1.5# -------------- [Demand Function]
#R=p xx x# ------------------ [Total Revenue ]
#R=(-0.0002x+1.5)xx x#
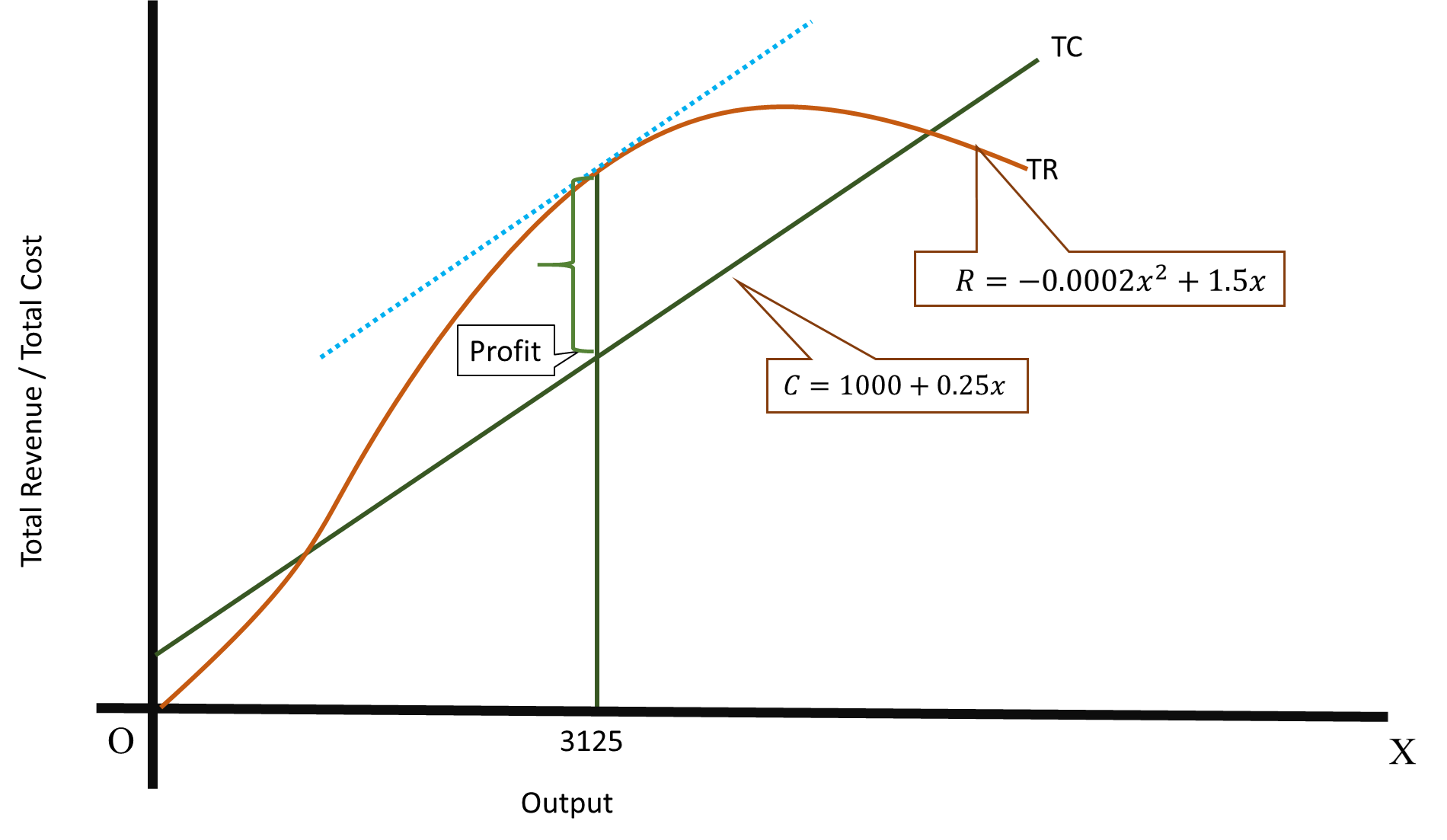
#R=-0.0002x^2+1.5x# ----------------- [Total Revenue Function]
C = Fixed Cost + Variable Cost
C=1000+0.25x -----------------------[Total Cost Function]
#pi= R -C# --------- Profit.
#pi=(-0.0002x^2+1.5x)-(1000+0.25x)#
#pi=-0.0002x^2+1.5x-1000-0.25x#
#pi=-0.0002x^2+1.25x-1000# --------------[Profit function]
#(dpi)/dx=-0.0004x+1.25#
At#(dpi)/dx=0=> -0.0004+1.25=0#
#x=(-1.25)/(-0.0004)=3125#
#(dpi^2)/(dx^2)=-0.0004 < 0#
At
Profit Maximising output
Substitute
#p=-0.0002x+1.5# -------------- [Demand Function]
#p=-0.0002(3125)+1.5=-0.625+1.5=0.875#
Profit maximising price is

