A composite geometric shape of triangle and rectangle is given with the proportionate relation given in the figure. Find angle #alpha# and #theta#?
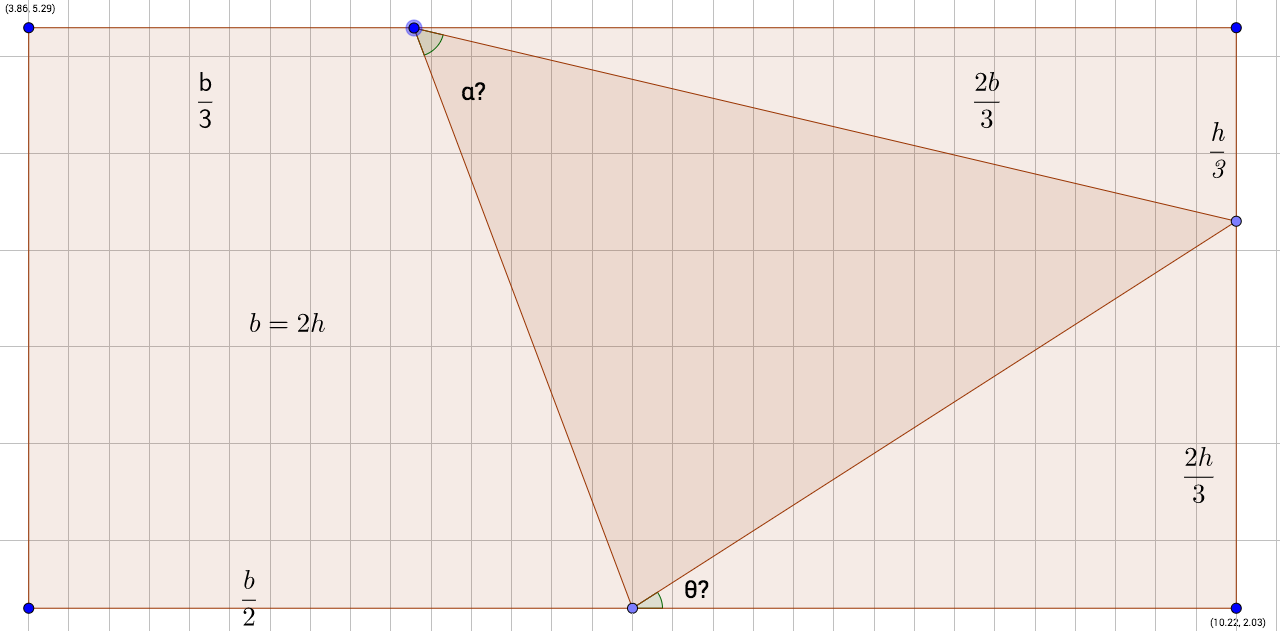
1 Answer
Explanation:
Labeling the picture as follows (with the additional constructed segment
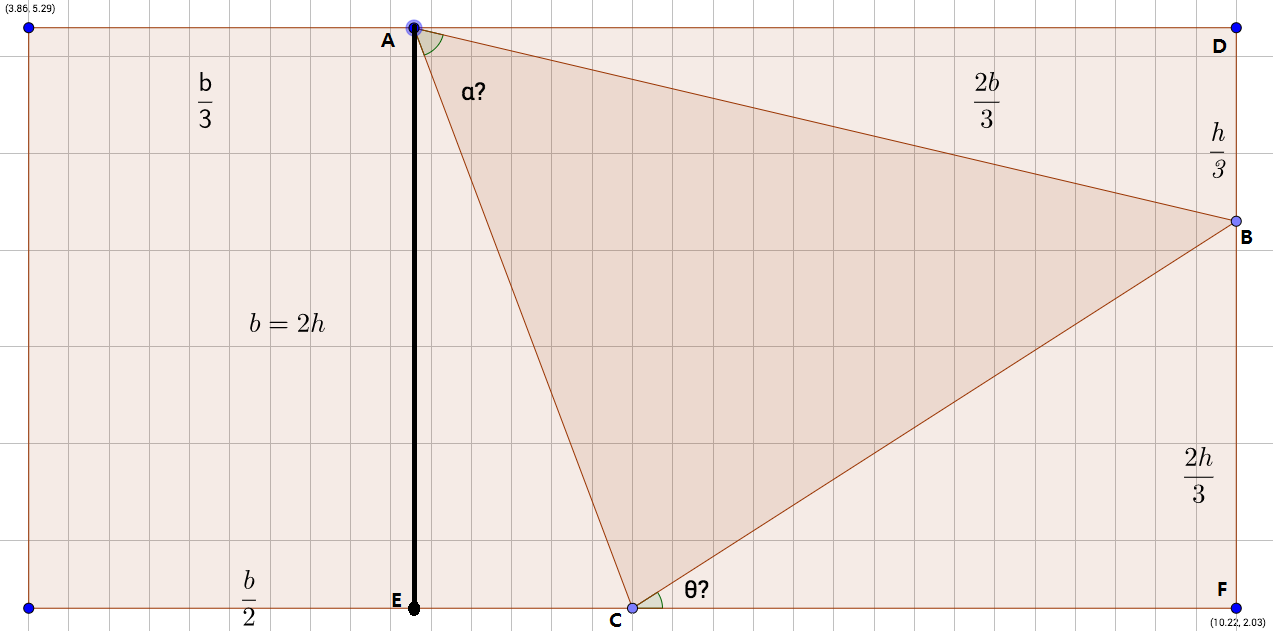
From the right triangle
Applying the inverse tangent function gives us
Note that
Together with
Additionally, as
Noting that

