A cone has a height of #6 cm# and its base has a radius of #6 cm#. If the cone is horizontally cut into two segments #3 cm# from the base, what would the surface area of the bottom segment be?
2 Answers
Yosief you answer is great but you just subtracted the original cone and the top cone. While that will give you a complete solution for the volume for the surface area you have three parts you need to consider:
1) The Base Area => this area of the circle
2) The side Area, that is the one you got by
3) Because you cut it now you have a smaller circle on top so you need to this area.
So using your terms
What changed? Well in your formula the first is the sum of squares instead the difference of squares. You were not that far you were a sign away from the correct answer. Make that change and voila you got it...
Surface area of bottom shape =
Explanation:
Let's start off by writing down what is already known and then finding some of the values we will need later.
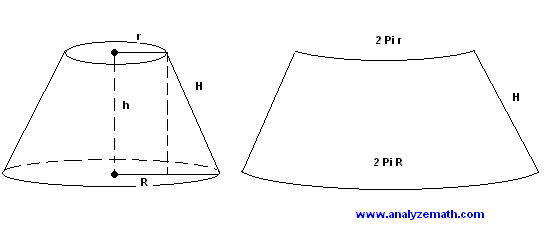
The BIG cone and the small cone are similar figures.
R = 6cm ; r = 3cm
H = 6cm ; h = 3cm
L =
Small cone:
surface area = area base + curved surface
s.a. =
Factorise to make it easier: s.a. =
In similar figures, the areas are in the same ratio as the square of the sides, length, radius etc.
BIG CONE: Surface area =
=
Surface area of fustrum (bottom segment);
BIG AREA - small area
=
=
However, the circular cut surface must be included as well.
Total Surface area =
=
=
=


