Question

A conical tank is 8m high. The radius at the top is 2m. At what rate is water running out if the depth is 3m and is decreasing at the rate of 0.4 m/min?

Answer 1

Rate `= (9pi)/40 \ m^3"min"^-1`
`\ \ \ \ \ \ \ = 0.707 \ m^3"min"^-1 \ \ \ \` (3dp)

Explanation:

Let us set up the following variables:

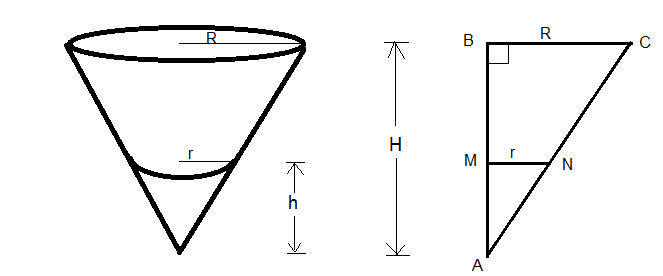
`{(R, "Radius of conical tank (m)",=2 \ m), (H, "Height of the conical tank (m)",=8 \ m), (t, "time", "(min)"), (h, "Height of water in cup at time t","(m)"), (r, "Radius of water at time t","(m)" ), (V, "Volume of water at time t", "(m"^3")") :}`

Our aim is to find `(dV)/dt` when `h=3` and we are given `(dh)/dt=0.4`

By similar triangles we have

`r:h = R:H`

`:. r/h=2/8 => r = h/4`

The volume of a cone is `1/3pir^2h`, So:

`V = 1/3 pi r^2 h`
`\ \ \ = 1/3 pi (h/4)^2 h`
`\ \ \ = 1/3 pi h^2/16 h`
`\ \ \ = (pi h^3)/48`

Differentiating wrt `h` we get:

`(dV)/(dh) = (pih^2)/16`

And Applying the chain rule we have:

`(dV)/(dt) = (dV)/(dh) * (dh)/(dt)`
`\ \ \ \ \ \ \= (pih^2)/16 * 0.4`
`\ \ \ \ \ \ \= (pih^2)/40`

And so when `h=3` we have:

`[ (dV)/(dt) ]_(h=3) = (pi(3^2))/40`
`" "= (9pi)/40 \ m^3"min"^-1`
`" "~~ 0.7068583 ... \ m^3"min"^-1`
`" "= 0.707 \ m^3"min"^-1 \ \ \ \` (3dp)