A diver breathing heliox with an oxygen composition of 5.0% wants to adjust the total pressure so that #P_(O_2)= "0.21 atm"#. What must the total pressure be?
1 Answer
The total pressure must be equal to 4.2 atm.
Heliox is a mixture of just two gases, helium and oxygen, so the total pressure in the tank must equal to the partial pressure of the helium plus the partial pressure of oxygen - this is known as Dalton's Law of partial pressures.
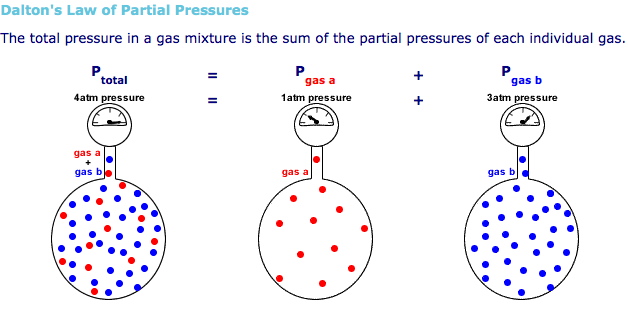
Mathematically, this can be written as
A more useful way of writing a relationship between the total pressure exerted by a gaseous mixture and the partial pressure of its individual components is to use something called the mole fraction.
For a gaseous mixture, the mole fraction is used to express the ratio between the number of moles of a gas and the total number of moles present in the mixture.
This means that you can write
In other words, the partial pressure of the oxygen will be equal to its mole ratio multiplied by the total pressure of the mixture.
In your case, you know that oxygen represents 5.0% of the mixture, the rest being helium. To make the calculations easier, you can assume that your mixture contains a total of 100 moles.
This means that your mixture contains 5 moles of oxygen (5% of 100 is 5). Therefore, the mole fraction of oxygen will be
As a result, the total pressure of the mixture has to be
The mole fraction of helium, for example, would be 0.95, because helium makes up 95% of the mixture. Its partial pressure would be
Notice that this is what you get when you use

