A farmer wants to enclose a 450,000m^2 rectangular field with fence. She then wants to sub-divide this field into three smaller fields by placing additional lengths of fence parallel to one of the side. How can she do this so that she minimizes the cost?
My equations are 450,000=xy and P=6x+4y, where x is the width and y is the length. However my teachers equation was different for the perimeter, his was P=4x+2y
My equations are 450,000=xy and P=6x+4y, where x is the width and y is the length. However my teachers equation was different for the perimeter, his was P=4x+2y
1 Answer
The minimum perimeter is given when
Explanation:
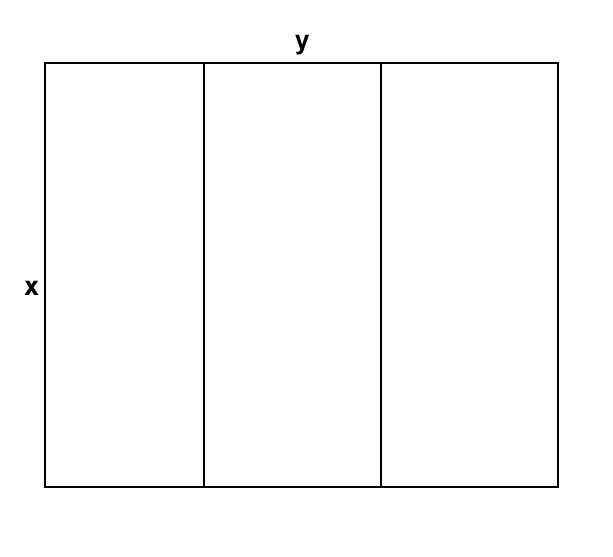
Without loss of generality let us assume that the field is divided as shown:
The area enclosed is given as
# xy=450000 => y=450000/x#
The total perimeter of all fencing is given by:
As indicated wlog we could interchange
# P=4x + 2*450000/x #
# \ \ \ =4x + 900000/x #
Differentiating wrt
# (dP)/dx =4 - 900000/x^2 #
At a critical point we have
# => 4 - 900000/x^2 = 0 #
# :. 900000/x^2 = 4 #
# :. x^2 = 900000/4 #
# :. x^2 = 225000 #
# :. x = 150sqrt(10) ~~ 474.3 => y ~~ 948.7#
This gives us
We can visually verify that this corresponds to a minimum by looking at the graph:
graph{4x + 900000/x [-10, 1000, -1000, 7830]}

