A farmer wants to wall off his four-sided plot of flat land. He measures the first three sides, shown as A, B, and C in the figure, where A = 4.99 km, B = 2.46 km, and C = 3.23 km and then correctly calculates the length and orientation of D?
A farmer wants to wall off his four-sided plot of flat land. He measures the first three sides, shown as A, B, and C in the figure, where A = 4.99 km, B = 2.46 km, and C = 3.23 km and then correctly calculates the length and orientation of the fourth side D.
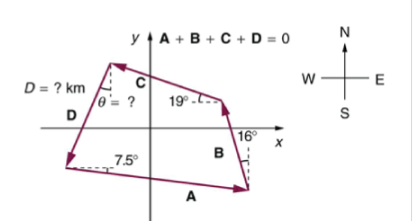
A: What is the length of the vector D in kilometers?
B: What is the orientation of the vector D, in degrees W of S?
A farmer wants to wall off his four-sided plot of flat land. He measures the first three sides, shown as A, B, and C in the figure, where A = 4.99 km, B = 2.46 km, and C = 3.23 km and then correctly calculates the length and orientation of the fourth side D.

A: What is the length of the vector D in kilometers?
B: What is the orientation of the vector D, in degrees W of S?
1 Answer
Magnitude:
Orientation:
Explanation:
Polar Representation:
All angles must be measured counter-clockwise from the positive direction of the X-axis (usually East)
Cartesian Representation:
Zero Displacement Condition:
Magnitude:
Orientation:
Note: In calculating the orientation, we recognize that the vector lies in the third quadrant because both the X and Y component are negative. Since the '

