Question

A ferris wheel with a radius of 10 m is rotating at a rate of one revolution every 2 minutes How fast is a rider rising when the rider is 16 m above ground level?

Answer 1

Great problem. It's a new-to-me kind of related rates.

Explanation:

Here is a sketch.

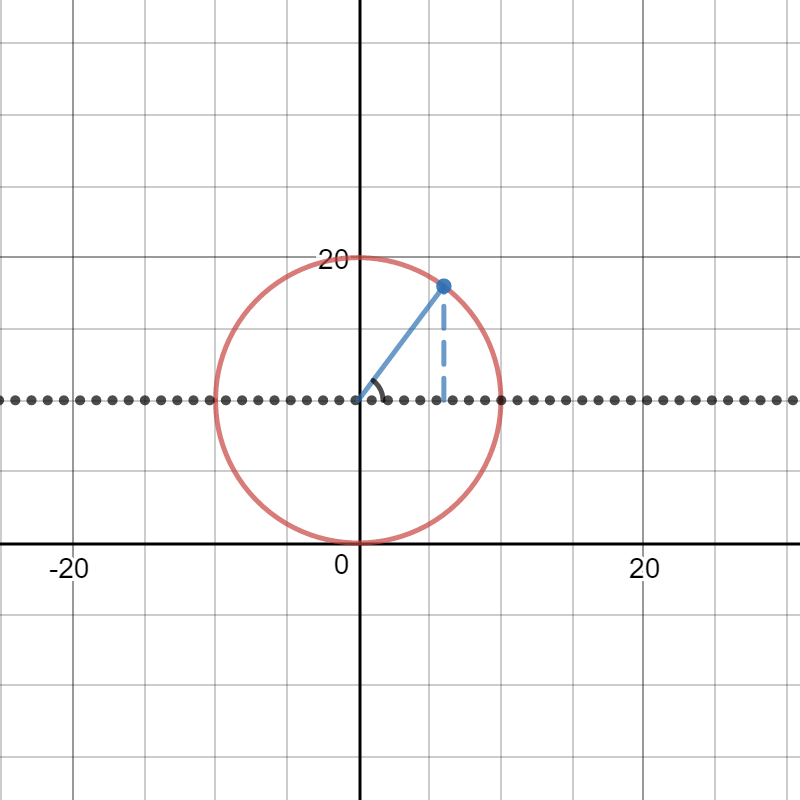
I'm sorry I can't label it clearly, but I'll talk through it.

The wheel is tangent to the ground and I've drawn a center line at `y=10`.

The rider is at the blue dot.

The radius (from `(0,10)` to the blue dot) is `10`.
The height above the line `y = 10` is the dashed blue line and I've called that `y`. (Perhaps not the best choice of variable names, but I'm using it.)

The central angle from the positive horizontal `y=10` to the rider is the angle of elevation. I've called it `theta`

`2` revolutions per minute gives us

`(d theta)/dt = (2pi)/2 "min" = pi` / `"min"`

The height above ground is `10 + y` and we want to know how fast it is changing when that height is `16` `m`.

That is the same as finding `dy/dt` when `y = 6`

So we have:

Variables `y` and `theta`

Rates of change `(d theta)/dt = pi` and find `dy/dt` when `y = 6`

Equation relating the variables:

`sin theta = y/10`

Solve the problem:

`y = 10 sin theta`

`d/dt(y) = d/dt(10sin theta)`

`dy/dt = 10cos theta (d theta)/dt`

When `y=6 =>sin theta = 6/10 = 3/5`.

So at that point `cos theta = 4/5` and

`dy/dt = 10(4/5)(pi) = 8pi` `m`/`min`

Notes for students

I've taught university and college calculus for years, but I had never seen this problem. So I had to approach it fresh.

You may find help and encouragement from these notes.

I started with a sketch of the wheel with its rider and the angle of elevation from the bottom of the wheel.
That led to some rather ugly calculations They could be done, but they were challenging.

In thinking about the rate of change of the angle I realized that I'd be better off staring my picture when the rider is 10 m above the ground.

Then the height became `10+y` and the rate of change of the angle was simplified.