A force field is described by #<F_x,F_y,F_z> = < xy , 2z-y^2 +x, 2y -zx > #. Is this force field conservative?
1 Answer
The force field is not conservative;
Explanation:
If
As stated above, the curl is given by the cross product of the gradient of
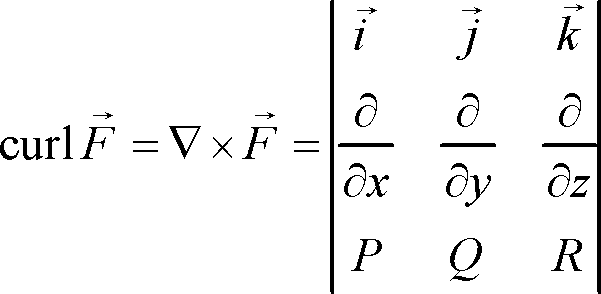
We have
The curl of the vector field is then given as:
#abs((veci,vecj,veck),(del/(delx),del/(dely),del/(delz)),(xy,2z-y^2+x,2y-zx))#
We take the cross product as we usually would with vectors, except we'll be taking partial derivatives each time we multiply by a partial differential.
For the
So far, so good.
For the
Remember that if we take the partial of a function with respect to some variable which is not present, the partial derivative is
#0# as we treat all other variables as constants.
For the
This gives a final answer of

