A gas has a solubility in water at 0°C of 3.5 g/L at a pressure of 0.80 atm. What pressure is needed to produce an aqueous solution containing 8.9 g/L of the same gas at 0°C?
1 Answer
Explanation:
You're dealing with pressures and gas solubility, which should automatically tell you that this is an example of a Henry's Law problem.
As you know, Henry's Law states that the solubility of a gas in a liquid is directly proportional to its partial pressure of the gas above the liquid.
#color(blue)("solubility " prop " partial pressure")#
This means that increasing the pressure of the gas above the liquid will Increase its solubility.
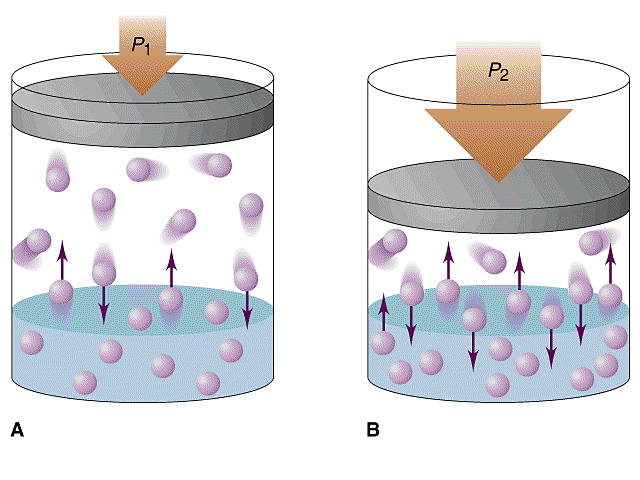
Likewise, decreasing the pressure of the gas above the liquid will decrease its solubility.
Mathematically, you can express Henry's Law like this
#color(blue)(S_1/P_1 = S_2/P_2)" "# , where
You'll often be dealing with the molar solubility of the gas, measured in moles per liter, but for this problem you can use the solubility in grams per liter.
So, the solubility of the gas increased from
Plug your values into the above equation and solve for
#P_2 = S_2/S_1 * P_1#
#P_2 = (8.9 color(red)(cancel(color(black)("g L"^(-1)))))/(3.5color(red)(cancel(color(black)("g L"^(-1))))) * "0.80 atm" = color(green)("2.0 atm")#
The answer is rounded to two sig figs.

