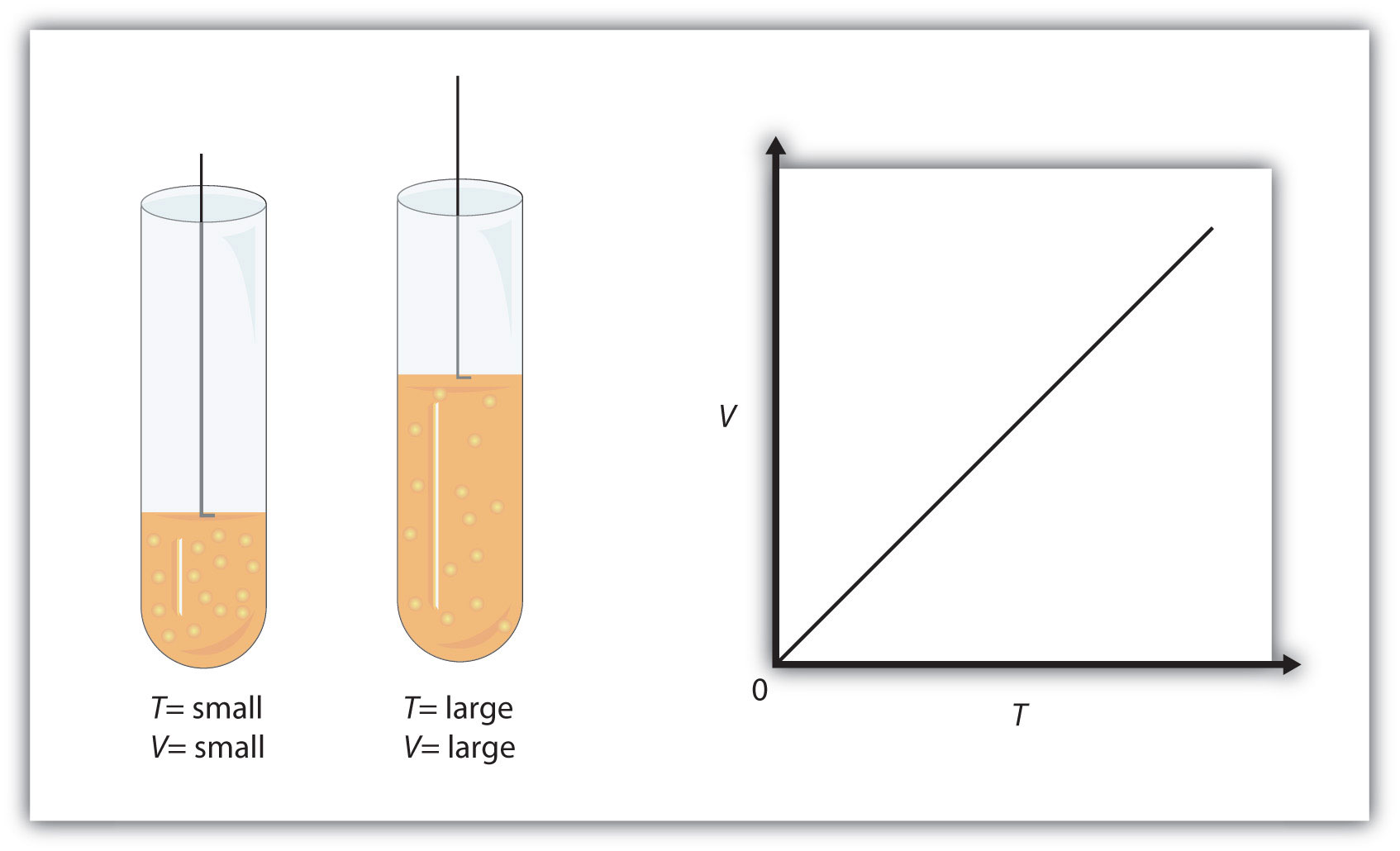
A gas thermometer contains 250 mL of gas at 0° C and 1.0 atm pressure. If the pressure remains at 1.0 atm, how many mL will the volume increase for every one celsius degree that the temperature rises?
I don't understand this part "for every one celsius degree"
I don't understand this part "for every one celsius degree"
1 Answer
Here's what I got.
Explanation:
The problem states that the pressure remains unchanged, so right from the start, you should know that you can use Charles' Law to calculate the change in volume associated with a
#color(blue)(ul(color(black)(V_1/T_1 = V_2/T_2)))#
Here
#V_1# and#T_1# represent the volume and the absolute temperature of the gas at an initial state#V_2# and#T_2# represent the volume and the absolute temperature of the gas at a final state
Now, it's very important to remember that you must work with absolute temperatures here, i.e. with temperatures expressed in Kelvin.
In your case, the gas starts at
#0^@"C" = 0^@"C" + 273.15 = "273.15 K"#
When the temperature of the gas increases by
#0^@"C" + 1^@"C" = 1^@"C" -># the temperatue increases by#1^@"C"#
which is
#1^@"C" = 1^@"C" + 273.15 = "274.15 K"#
Similarly, you will have
#"273.15 K" + "1 K" = "274.15 K" -># the temperature increases by#"1 K"#
So, you must determine the change in volume that accompanies a
Rearrange the equation to solve for
#V_1/T_1 = V_2/T_2 implies V_2 = T_2/T_1 * V_1#
Plug in your values to find
#V_2 = (274.15 color(red)(cancel(color(black)("K"))))/(273.15color(red)(cancel(color(black)("K")))) * "250 mL" = "250.9 mL"#
So the volume of the gas increased by
#overbrace("250.9 mL")^(color(blue)("at 274.15 K" = 1^@"C")) - overbrace("250 mL")^(color(blue)("at 273.15 K" = 0^@"C")) = "0.9 mL"#
Notice what happens when you increase the temperature from
#V_2 = (275.15 color(red)(cancel(color(black)("K"))))/(274.15 color(red)(cancel(color(black)("K")))) * "250.9 mL" = "251.8 mL"#
The volume of the gas increased by
#overbrace("251.8 mL")^(color(blue)("at 275.15 K" = 2^@"C")) - overbrace("250.9 mL")^(color(blue)("at 274.15 K" = 1^@"C")) = "0.9 mL"#
You can thus say that with every
If you were to draw a graph of this relationship, you'd end up with a straight line that goes