Question

A large vase has a square base of side length 6 cm, and flat sides sloping outwards at an angle of 120◦ with the base. How to find the rate when height is rising?

A large vase has a square base of side length 6 cm, and flat sides sloping outwards at an angle of 120◦ with the base. Water is flowing in at 12cm3/s.

How to find, to three significant figures, the rate at which the height of water is rising when the water has been flowing in for 3 seconds.

Answer 1

`dh/dt=0.246 cms^-1`

Explanation:

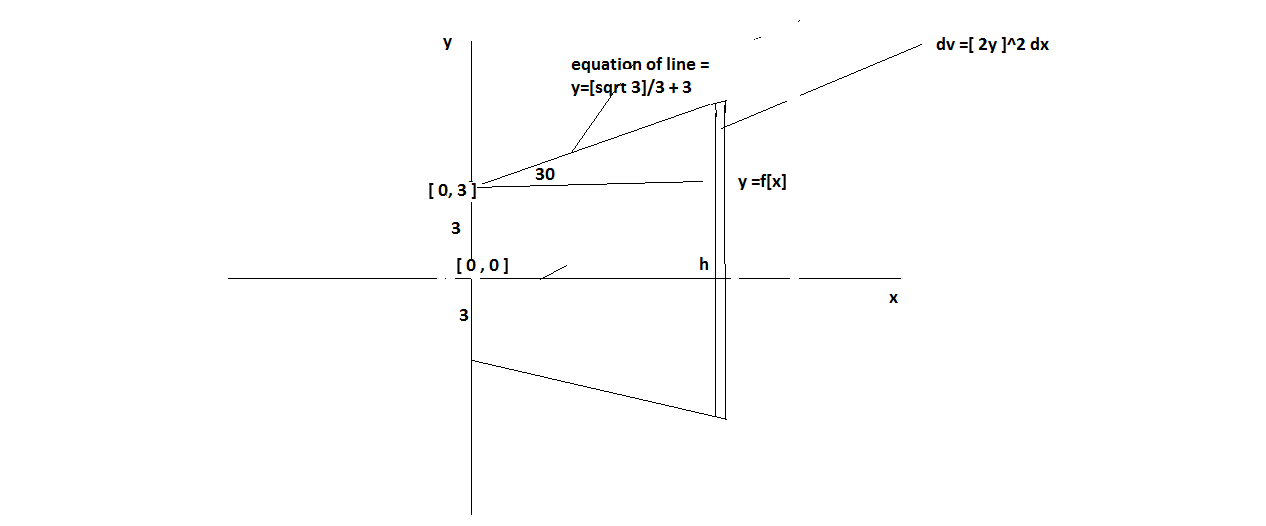From the sketch it can be seen that an element of volume `dv` = `[2y]^2dx` We need to integrate `[2y^2]dx` from `0` to `h`., so we need to find `y` in terms of `x`.

It can be seen that the straight line along the face of the pyramid has equation `y=sqrt3/3x+3`..........`[1]` [ since tan`pi/6`,i.e, tan 30 degrees =`sqrt3/3` and the `y` intercept is `[0,3]`

`[2y]^2` = `[2[sqrt3/3x +3]]^2` = `[ 4x^2/3+ 8sqrtx+36]`.........`[2]`

Thus volume of the frustrum of the pyramid `V` =`int_0^h[[4x^2]/3 + 8sqrt3 + 36]dx` = `[[4h^3]/9 + [4sqrt3]h^2 +36h]......`[3]##

From the question `dv/dt = 12cm^3s^-1` so after `3` seconds the volume `V` = `36 cm^3`

Therefore, `36 = [4h^3]/9 +[4sqrt3]h^2 + 36h`. Solving this cubic for `h` yields a real value of `h` = `0.85249` [ online cubic equation solver].

Differentiating.......`[3]` wrt to t.

`[dv]/dt= 4/3h^2[dh/dt] + 8sqrt3hdh/dt+36dh/dt`.

`[dv]/dt= [dh]/dt[ 4/3h^2+8sqrt3h+36]` But `dv/dt =12` [from the question]

Therefore, `[dh]/dt=12/[ 4/3h^2 + 8sqrt3h+36]`, and evaluated when `h` = `0.85249` will give the answer above. Hope this was helpful, and I believe it to be correct. I will ask it to be checked.