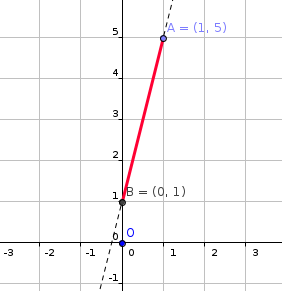
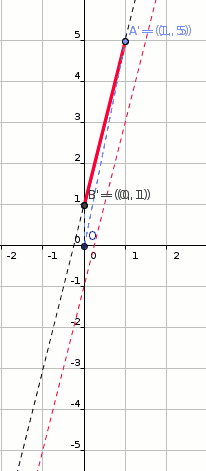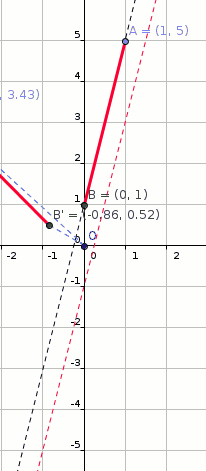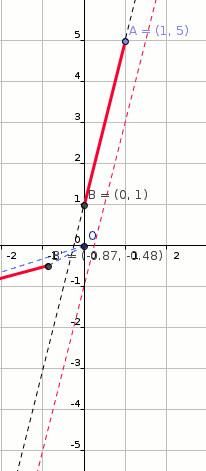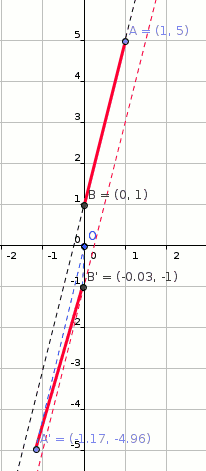
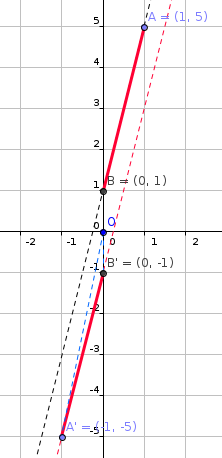
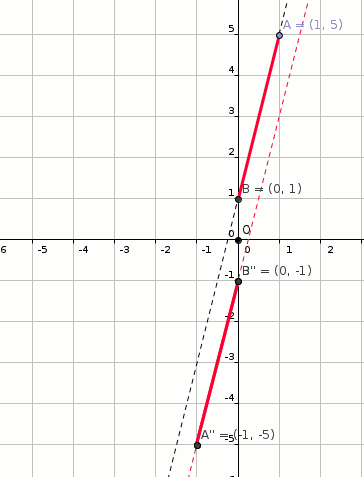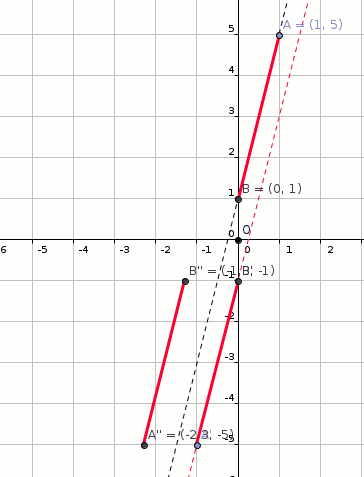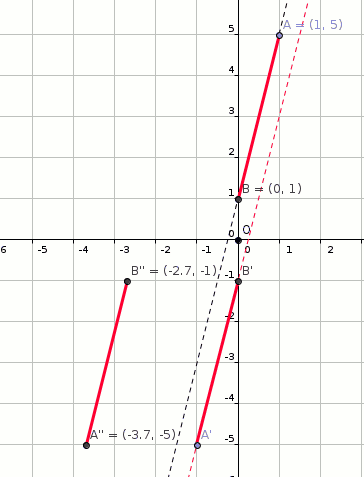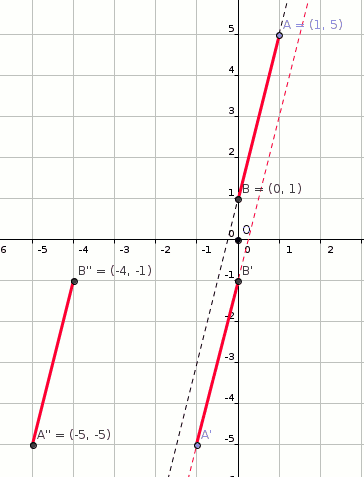
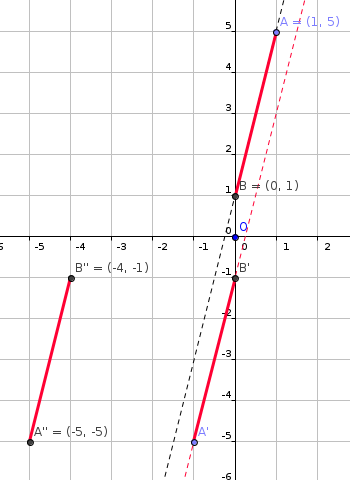
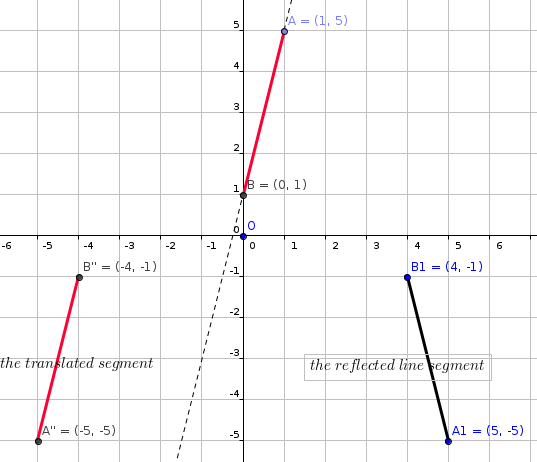
A line segment has endpoints at #(1 ,5 )# and #(0 ,1 )#. If the line segment is rotated about the origin by # pi #, translated horizontally by # - 4 #, and reflected about the y-axis, what will the line segment's new endpoints be?

Question

2417 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-27T21:15:43

#"the line segment's new end points are:"A1(5,-5) " and "B1(4,-1)#

enter image source here

#"first; draw line segment AB like figure above"#

#"now rotate the line segment about the origin by "pi #

enter image source here

#"now "A(1,5) rArr " "A'(-1,-5)#

#B(0,1) rArr" "B'(0,-1)#

enter image source here

#"translate horizontally by -4"#

#"now "A'(-1,-5) " is " A''(-1-4,-5)=(-5,-5)#
#B'(0,-1) " is " B''(0-4,-1)=(-4,-1)#

enter image source here

#"finally; reflect the line segment about y-axis"#

enter image source here