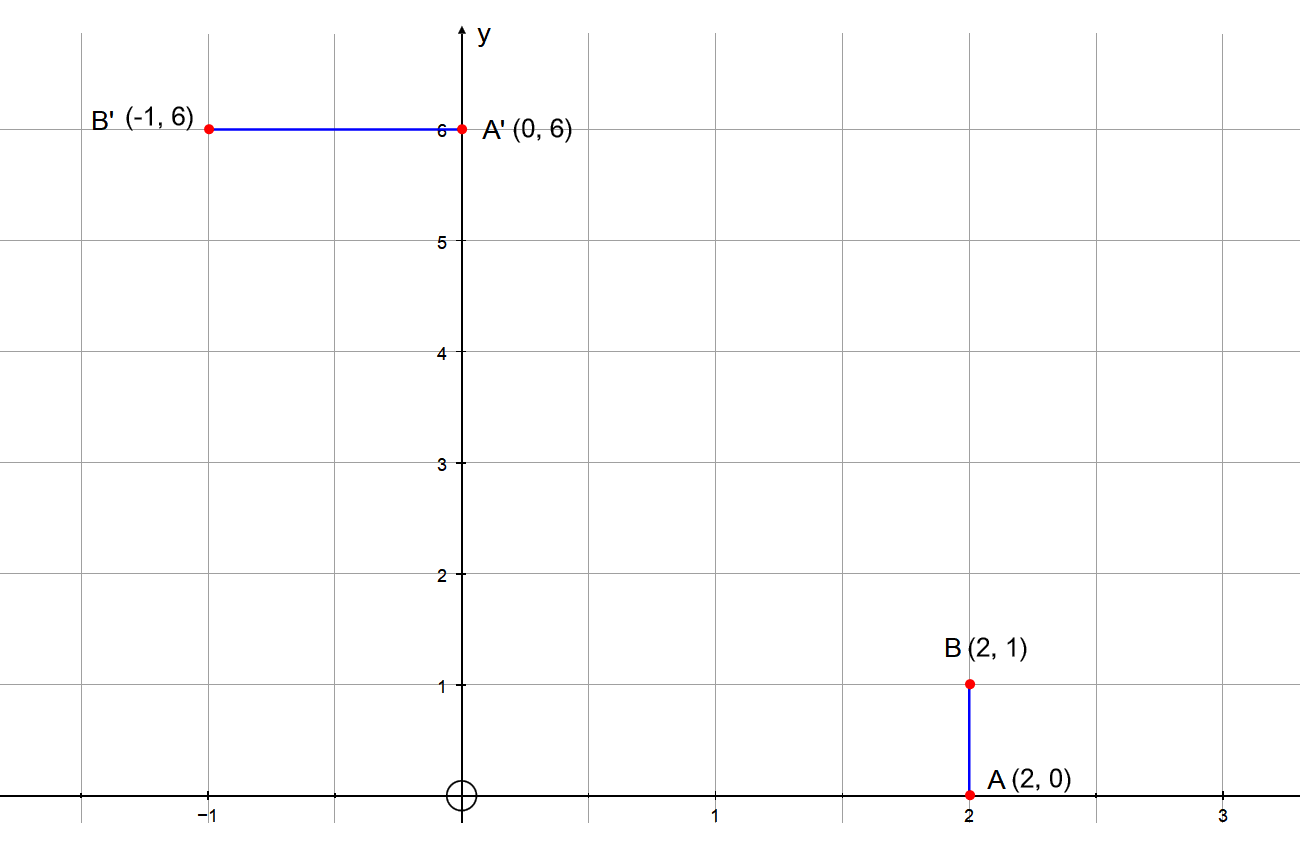
A line segment has endpoints at #(2 ,0 )# and #(2 ,1 )#. If the line segment is rotated about the origin by #( pi)/2 #, translated vertically by #-8 #, and reflected about the x-axis, what will the line segment's new endpoints be?

Question

1295 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-11T12:26:42

#color(blue)(A'=(0,6)#

#color(blue)(B'=(-1,6)#

No direction of rotation has been given, so I will take this as anti-clockwise.

Let #A=(2,0), B=(2,1)#

A rotation about the origin by #pi/2# radians maps:

#(x,y)->(-y,x)#

A translation by #-8# units in the vertical directions maps:

#(x,y)->(x,y-8)#

A reflection in the x axis maps:

#(x,y)->(x,-y)#

We can put all these mappings together:

#(x,y)->(-y,x)->(-y,x-8)->(-y,-(x-8))#

#A->A'=(2,0)->(-(0),-(2-8))=(0,6)#

#B->B'=(2,1)->(-(1),-((2-8))=(-1,6)#

PLOT:

enter image source here