Question

A line segment is bisected by a line with the equation `3 y - 8 x = 2`. If one end of the line segment is at `(1 ,3 )`, where is the other end?

Answer 1

The other end is at the point: `(57/73,225/73)`

Explanation:

When given a the equation of a line in standard form:

`ax + by = c" [1]"`

All lines perpendicular to the given line will be of the form:

`-bx + ay = k" [2]"`

where k is an arbitrary constant.

Write the given equation for the bisecting line in standard form:

`8x - 3y = -2" [3]"`

Write the equation for all lines perpendicular to equation [3]:

`3x + 8y = k" [4]"`

The start of the bisected line segment, `(x_"start", y_"start")`, is given as the point `(1, 3)`

Substitute 1 for x and 3 for y into equation [4] and solve for k:

`3(1) + 8(3) = k`

`k = 27`

The equation of the bisected line segment is:

`3x + 8y = 27" [5]"`

Add 8 times equation [3] to 3 times equation [5]:

`64x - 24y + 9x + 24y = -16 + 81`

`73x = 65`

`x_"intersect" = 65/73`

The x coordinate of the end can be found by adding the start coordinate to twice the change for the point of intersection:

`x_"end" = x_"start" + 2(x_"intersect" - x_"start")`

`x_"end" = x_"start" + 2x_"intersect" - 2x_"start")`

`x_"end" = 2x_"intersect" - x_"start"`

`x_"end" = 2(65)/73 - 1`

`x_"end" = 57/73`

Substitute `57/73` for x in equation [5] and the solve for the value of `y_"end"`

`3(57/73) + 8y_"end" = 27`

`y_"end" = 27/8 - 3/8(57/73)`

`y_"end" = 225/73`

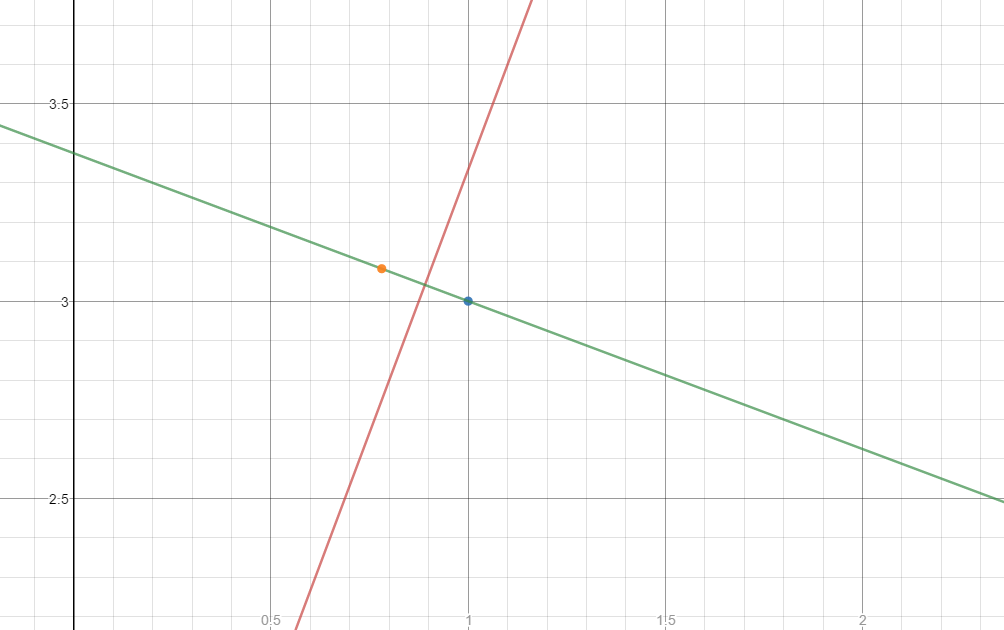
Here is a graph of, the two lines, the start point, and the end point.