A long rectangular sheet of metal, 12cm wide, is to be made into a rain gutter by turning up two sides which make an angle of 120 degrees with the base. How many cm should be turned up to give the gutter its greatest capacity?
1 Answer
Nov 30, 2015
First, draw a sketch of the problem
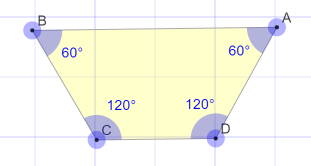
Explanation:
This is an isosceles trapezoid with equal sides BC and AD
The length base CD
If you draw a perpendicular from C to BA, that will be the height
Length of base BA
Area of trapezoid
Insert the known values into the area formula ...
Area
Area
Now, take the derivative with respect to x and set equal to zero ...
Solution :

