Question

A man pulls his child in a sled at a constant velocity. The child and sled have a combined mass of 60 kg. The force applied on the handle is 200N at an angle of 15. Draw a free body diagram. What is the normal force acting on the sled?

What is the force of friction acting on the sled?

Answer 1

With this kind of problem, it's very important that you keep track of your sign conventions. I set the y direction perpendicular (outwards from) to the ramp as positive and x direction parallel down the ramp as negative. Thus, `vecg < 0` in this convention.

Here's the free body diagram I came up with (treat the sled and child as one unified object):

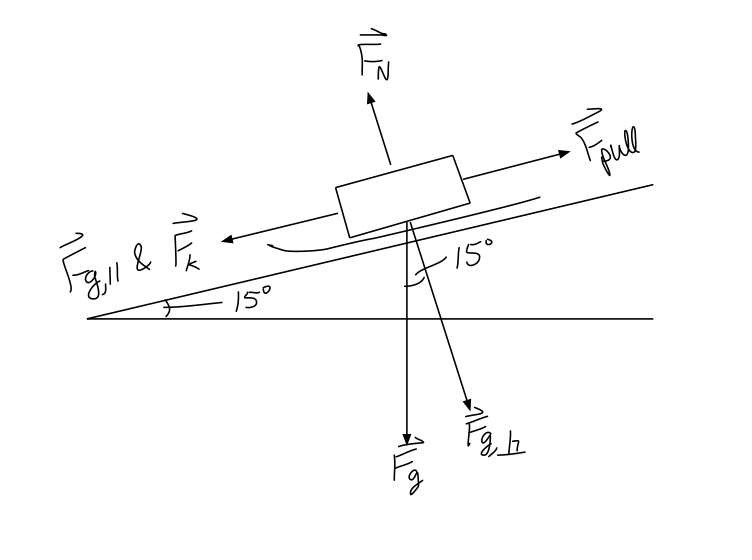
Remember that `vecF_(g,||) = mvecgsintheta` is the parallel force component due to gravity that opposes the pulling force and `vecF_(g,_|_) = mvecgcostheta` is the perpendicular force component due to gravity that opposes the normal force.

Therefore, numerically, `vecF_(pu ll)` and `vecF_k` oppose each other, and numerically, `vecF_N` and `mvecgcostheta` oppose each other, and we can write a sum of the forces:

`sum_i vecF_(x,i) = -vecF_k + vecF_(pu ll) + mgsintheta = 0`

`sum_i vecF_(y,i) = vecF_N + mgcostheta = 0`

where `vecF_k` is the reacting force of the kinetic friction, `vecF_(pu ll) = "200 N"` is the force used to pull the sled, and `vecF_(g,||) = mgsintheta` is the force component of gravity parallel to the ramp. Note that `veca_x = 0` due to the constant velocity.

The plus and minus signs in the equations are such that the forces numerically oppose each other when they add later on. I know that `vecF_N > 0` and `mu_k > 0`, so `vecF_k > 0` (the minus sign accounts for left being negative). The reason why `mgsintheta` in the same direction has a plus sign is because `vecg < 0` already.

You can see we can solve for the normal force right away.

`color(blue)(vecF_N) = -mgcostheta`

`= -("60 kg" xx -"9.81 m/s"^2 xx cos(15^@)) = color(blue)("568.54 N")`

Once we have that, we should recall the definition of the kinetic friction force:

`vecF_k = mu_kvecF_N`,

where `mu_k` is the coefficient of kinetic friction.

Thus, the coefficient of kinetic friction is acquired like so:

`-vecF_k + vecF_(pu ll) + mgsintheta = 0`

`-vecF_k = -vecF_(pu ll) - mgsintheta = -mu_kvecF_N`

`color(blue)(mu_k) = (vecF_(pu ll) + mgsintheta)/vecF_N`

`= (("200 N") + ("60 kg")(-"9.81 m/s"^2)sin(15^@))/("568.54 N")`

`= color(blue)(0.0838)`

And the force of kinetic friction would be:

`color(blue)(vecF_k) = vecF_(pu ll) + mgsintheta`

`= "200 N" + ("60 kg")(-"9.81 m/s"^2)(sin15^@)`

`=` `color(blue)("47.66 N")`