A man standing on a wharf is hauling in a rope attached to a boat, at the rate of 4 ft/sec. if his hands are 9 ft. above the point of attachment, what is the rate at which the boat is approaching the wharf when it is 12 ft away?

Question

11750 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-01-22T17:30:07

#sf(-5" ft/s")#

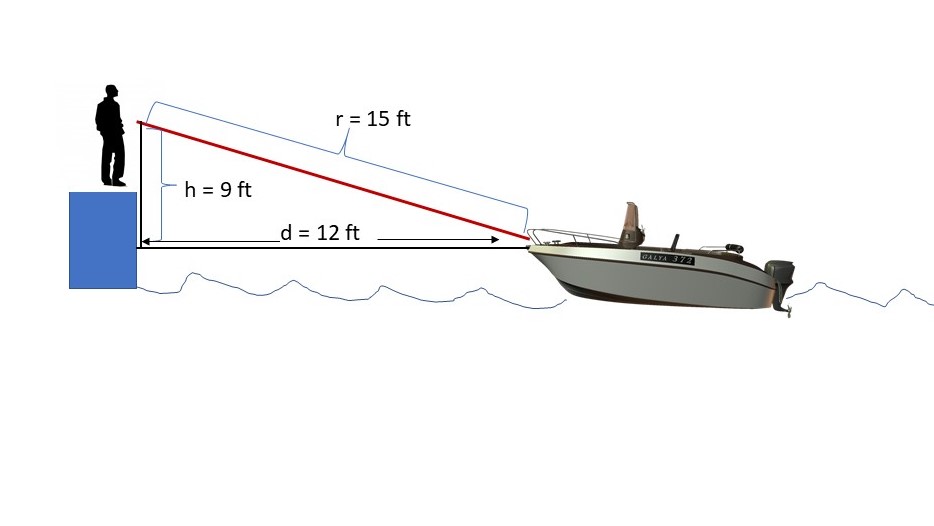
MFDocs

We are told:

#sf((dr)/dt=-4color(white)(x)"ft/s")#

We need to find #sf((d(d))/dt)#

Pythagoras gives us the value of r at that particular instant:

#sf(r^2=h^2+d^2)#

#sf(r^2=9^2+12^2)#

#sf(r^2=81+144)#

#sf(r=15 color(white)(x)ft)#

We know that:

#sf(r^2=81+d^2)#

Differentiating implicitely with respect to t:

#sf(2r.(dr)/dt=2d.(d(d))/dt)#

Putting in the numbers#rArr#

#sf(2xx15xx-4=2xx12.(d(d))/dt)#

#sf(-120/24=(d(d))/dt)#

#sf((d(d))/dt=-5color(white)(x)"ft/s")#