A mixture of #H_2# and water vapor is present in a closed vessel at 20°C. The total pressure of the system is 755.0 mmHg. Partial pressure of water vapor at 20°C equals 17.5 mmHg. What is the partial pressure of #H_2#?
1 Answer
Explanation:
The idea here is that the total pressure of the system will be equal to the sum of the partial pressures of each gaseous component of the system, as given by Dalton's Law of Partial Pressures.
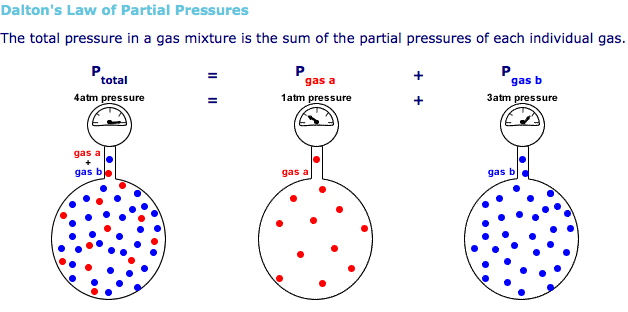
In your case, you have
#P_ "total" = P_ ("H"_ 2) + P_ ("H"_ 2"O")#
Here
That happens because when temperature and volume are kept constant, the pressure of a gas is directly proportional to the number of moles present.
In other words, more moles of gas will result in a proportional increase in the pressure exerted by the gas.
Simply put, the pressure you'd get if the number of moles of hydrogen gas were isolated in the same volume and kept under the same temperature will be equal to the partial pressure of hydrogen gas in the mixture.
The same thing can be said for the water vapor. Isolating the water vapor in the same volume and under the same temperature will give you a pressure that is equal to the partial pressure of water vapor in the mixture.
Therefore, the partial pressure of hydrogen gas in this mixture is
#P_ ("H"_ 2) = "755.0 mmHg" - "17.5 mmHg" = color(green)(|bar(ul(color(white)(a/a)color(black)("737.5 mmHg")color(white)(a/a)|)))#

