A particle of mass m moving with a velocity v makes an elastic one-dimensional collision with a stationary particle of mass m establishing a contact with it for extremely small time T. Their force of contact increases from zero to ...........?
A particle of mass #m# moving with a velocity #v# makes an elastic one-dimensional collision with a stationary particle of mass #m# establishing a contact with it for extremely small time #T# . Their force of contact increases from zero to #F_0# linearly in time T/4, remains constant for a further time #T/2# and decreases linearly from #F_0# to zero in further time #T/4# as shown in figure. The magnitude possesssed by #F_0# is ?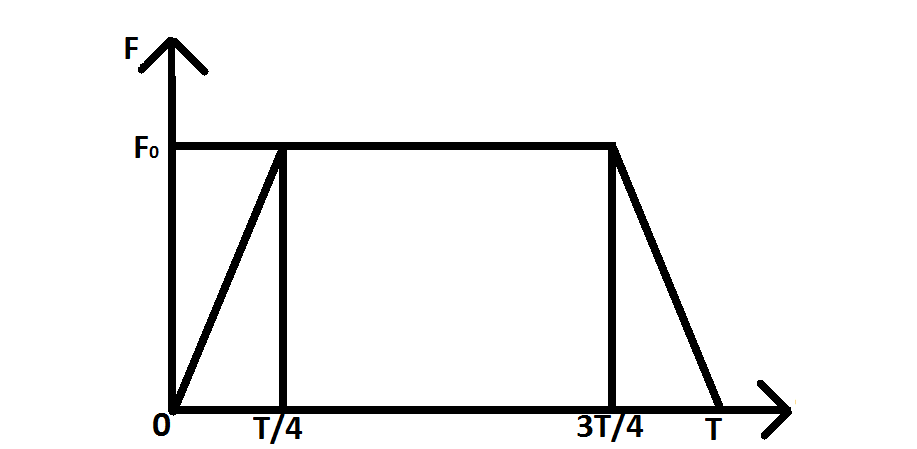
A particle of mass 
1 Answer
Explanation:
Momentum is always conserved so we can say -- where
From conservation of (kinetic) energy, we can say:
From
From
or
From a consideration of the physical setup, we see that the only practical conclusion is that:
The first particle cannot just move through the second particle with the second remaining stationary. Rather, all momentum and energy is transferred to the second particle.
We now turn to Netwon's 2nd Law:
Because we have a Force-time graph, we can tweak the second law as follows, by integrating wrt time:
We do this because we see that
For the second integration, we change the integration variable (using the chain rule) to get:
Which here, because
Thus we can say that:
Or:

