Question

A physical fitness room consists of a rectangular region with a semicircle on each end. If the perimeter of the room is to be a 200 meter running track, how do find the dimensions that will make the area of the rectangular regions as large as possible?

Answer 1

# { ("length", =50 \ m), ("width", =50/pi \ m ~~ 15.92 \ m) :} #

Explanation:

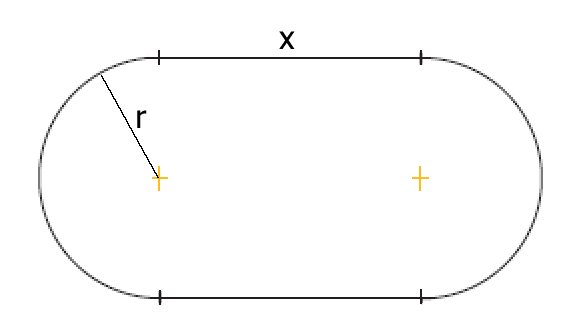
Let us set up the following variables:

# { (x, "length of rectangular region (m)"), (r, "Radius of semi-circle (m)"), (P, "Total perimeter of the room (m"^2")"), (A, "Total Area of the rectangular region (m"^2")") :} #

The perimeter of the given room, is that of two identical semicircular ends, and the two rectangular region lengths. Thus:

`P = 1/2(2pir) + 1/2(2pir) + x + x`

`\ \ \= 2pir + 2x`

But we are given that the total perimeter is `200 \ m`, a constant, therefore:

`2pir + 2x =200 => r = (100-x)/(pi)`

Now the total area of the rectangular region is:

`A = (x)(2r)`
`\ \ \ = (x)2((100-x)/(pi))`
`\ \ \ = (200x-2x^2)/(pi)`

For maximum or minimum, we seek a critical point of the area function, `A(x)` wrt `x`. We therefore calculate the derivative:

`(dA)/dx = (200-4x)/pi`

At a critical point, the first derivative vanishes, thus we require:

`f'(x) = 0 => 200-4x=0`

`:. x=50 \ m`

We can visually confirm from the graph:
graph{(200x-2x^2)/(pi) [-50, 150, -400, 2000]}

With `x=50 => r = (100-50)/(pi) = 50/pi`

that the solution is both consistent and corresponds to a maximum, and the dimensions of the sought room are thus:

# { ("length", =x, =50 \ m), ("width", =2r,=50/pi \ m ~~ 15.92 \ m) :} #