Question

A piece of wire 60 cm in length is cut into two pieces. The first piece forms a rectangle 5 times as wide as it is long. The second piece forms a square. Where should the wire be cut to? 1)minimize the total area 2)maximize the total area

Answer 1

Max Area: `"225 cm"^3`
Min Area: `"80.36 cm"^3`

Explanation:

Steps:

1) Draw out a rectangle and a square

2) Label all your variables based on the information from the question

• Since the length of the rectangle is five times as the width. Therefore, we know that `5x` is the length and `x` is the width.
• Since it is a square and we do not know the values of the sides, we can label the sides as `y`.

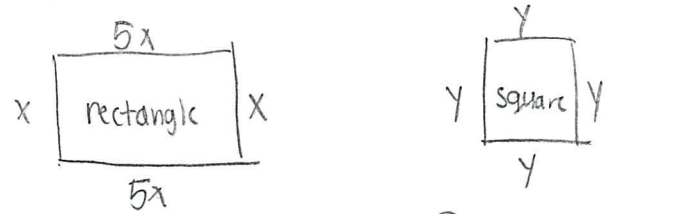
3) Find the helper equation for the equation which you are trying to optimize

• The wire `"60 cm"` is the circumference for both the rectangle and the square
• `12x+4y=60`

4) Find the equation for `y` of the helper equation in terms of `x`

• `y = 15-3x`

5) Find the equation that you are trying to optimize

• `"Area" = AR + AS = 5x^2 + y^2`

6) Plug the equation of `y` into the equation you are trying to optimize

• `5x^2 + y^2`
• `5x^2 +(15-3x)^2 = 14x^2-90x+225`

7) Take the derivative of the equation and find the critical point(s) while determine whether they are max or min

`A' = 28x-90`

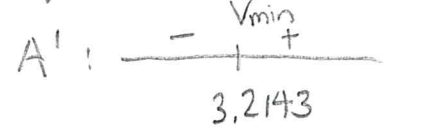
8) Check the endpoints!

Endpoints indicate the maximum and minimum value you can have for the rectangle

• `12x = 60, x = 5` <-- indicating all material used to create the rectangle
• `x = 0` <-- indicating all material used to create the square

9) Find the answers by plugging in endpoints and critical number into the original area equation

• `A(3.2143) = "80.36 cm"^3`
• `A(0) = "225 cm"^3`
• `A(5) = "125 cm"^3`

Therefore, the maximum of the total area we have is `"225 cm"^3` and the minimum value we have is `"80.36 cm"^3`.

Answer 2

`38.4 or 21.6 cm` for a minimum area of `80.4 cm^2`
The limit as `x -> 0` is `225 cm^2`

Explanation:

The total length is 60. The first rectangle has dimensions of `x xx 5x`, and the perimeter is thus `2(x + 5x) = 12x`. The remaining length for the square is then `60 – 12x`. This is equal to the square perimeter, `4y`, so we can express the square side ‘y’ in terms of ‘x’ as `4y = 60 – 12x` ; `y = 15 – 3x`. The square area in terms of ‘x’ is thus `(15 – 3x)^2` = `9x^2 – 90x +225`.

Combined with the area of the rectangle we obtain the total area as:
`A_t = 5x^2 + 9x^2 – 90x +225` = `14x^2 – 90x + 225` This quadratic indicates that it will only have one extrema – the minimum for a given length of wire. That point is where the first derivative of the area quadratic equation is zero. `f’(x) = 28x – 90` Minimum at `x = 3.2`

The derived dimensions follow:
Rectangle short side: `x = 3.2cm`
Rectangle long side: `5x = 16cm`
Rectangle area: `51.2 cm^2`
Square side: `y = 15 – 3x = 5.4`
Square area: `29.2 cm^2`
Total Area: `80.4 cm^2`
Total lengths: `2(3.2 + 16) + 4(5.4) = 38.4 + 21.6 = 60` Correct. Cut the wire at a length of `60 – 12x = 60 – 38.4 = 21.6cm or 38.4cm`