Question

A pilot flies horizontally at 840 km/h, at height h = 48 m above initially level ground. However, at time t = 0, the pilot begins to fly over ground sloping upward at angle θ = 5.9° ?

Answer 1

The plane will hit the hill in `"1.99 s"`.

Explanation:

FULL QUESTION

A pilot flies horizontally at `"840 km/h"`, at height `h = "48 m"` above initially level ground. However, at time `t = 0`, the pilot begins to fly over ground sloping upward at angle `theta = 5.9^@`.

If the pilot does not change the airplane's heading, at what time t does the plane strike the ground?

`stackrel("----------------------------------------------------------------------------------------------------------------")`

The idea here is that you can use the angle the slope makes with the horizontal to determine the distance the plane covers before hitting the side of the hill.

Assuming that the horizontal speed of the plance does not change, you can then use this distance to find the time it takes the plane to hit the hill.

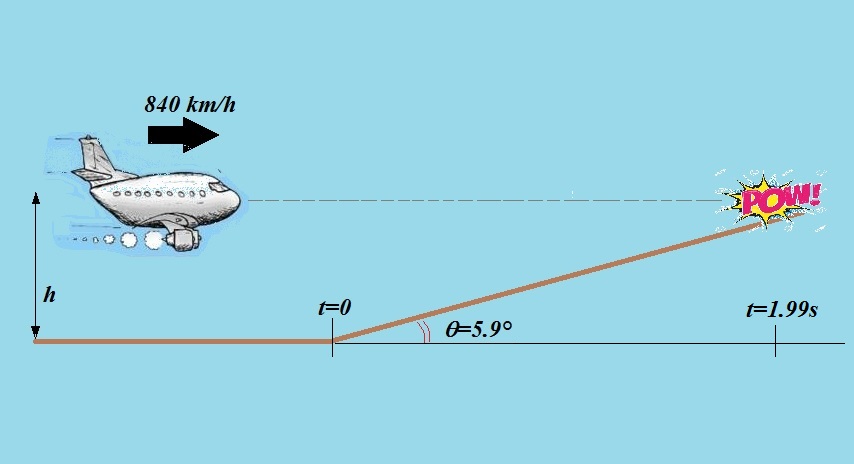
So, at `t=0`, the plane starts flying over ground that slopes upward at an angle `theta = 5.9^@` with the horizontal.

If it covers a distance `d` after this point in time, then you can use

`tantheta = h/d" "`, where

`h` is the height at the moment it starts to fly over the hill.

This means that the plane will travel

`d = h/tantheta = "48 m"/tan(5.9^@) = "48 m"/0.10334 = "464.5 m"`

Now, you need to convert its speed from kilometers per hour to meters per second before moving on

`840color(red)(cancel(color(black)("km")))/color(red)(cancel(color(black)("h"))) * "1000 m"/(1color(red)(cancel(color(black)("km")))) * "1 h"/"3600 s" = "233.3 m/s"`

Since the plane's horizontal speed is presumed constant, you have

`v = d/t implies t = d/v`

`t = (464.5color(red)(cancel(color(black)("m"))))/(233.3color(red)(cancel(color(black)("m")))/"s") = color(green)("1.99 s")`