Question

A plane flying horizontally at an altitude of 1 mi and speed of 500mi/hr passes directly over a radar station. How do you find the rate at which the distance from the plane to the station is increasing when it is 2 miles away from the station?

Answer 1

When the plane is 2mi away from the radar station, its distance's increase rate is approximately 433mi/h.

Explanation:

The following image represents our problem:

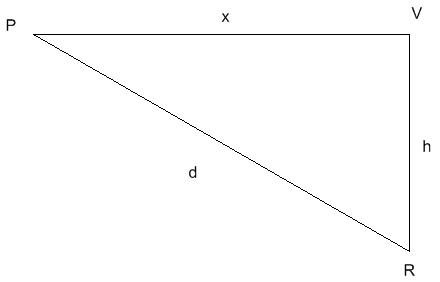
P is the plane's position
R is the radar station's position
V is the point located vertically of the radar station at the plane's height

h is the plane's height
d is the distance between the plane and the radar station
x is the distance between the plane and the V point

Since the plane flies horizontally, we can conclude that PVR is a right triangle. Therefore, the pythagorean theorem allows us to know that d is calculated:

`d=sqrt(h^2+x^2)`

We are interested in the situation when d=2mi, and, since the plane flies horizontally, we know that h=1mi regardless of the situation.

We are looking for `(dd)/dt=dotd`

`d^2=h^2+x^2`

`rarr (d(d^2))/dt=(d(d^2))/(dd)(dd)/dt=cancel((d(h^2))/(dh)(dh)/dt)+(d(x^2))/(dx)(dx)/dt`

`=2d dotd=2xdotx`

`rarr dotd=(2xdotx)/(2d)=(xdotx)/d`

We can calculate that, when d=2mi:

`x=sqrt(d^2-h^2)=sqrt(2^2-1^2)=sqrt3` mi

Knowing that the plane flies at a constant speed of 500mi/h, we can calculate:

`dotd=(sqrt3*500)/2=250sqrt3~~433` mi/h