A plane flying horizontally at an altitude of 1 mi and speed of 500mi/hr passes directly over a radar station. How do you find the rate at which the distance from the plane to the station is increasing when it is 2 miles away from the station?
1 Answer
When the plane is 2mi away from the radar station, its distance's increase rate is approximately 433mi/h.
Explanation:
The following image represents our problem:
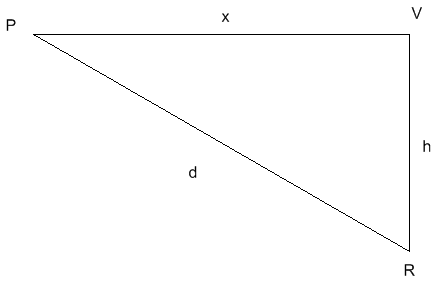
P is the plane's position
R is the radar station's position
V is the point located vertically of the radar station at the plane's height
h is the plane's height
d is the distance between the plane and the radar station
x is the distance between the plane and the V point
Since the plane flies horizontally, we can conclude that PVR is a right triangle. Therefore, the pythagorean theorem allows us to know that d is calculated:
We are interested in the situation when d=2mi, and, since the plane flies horizontally, we know that h=1mi regardless of the situation.
We are looking for
We can calculate that, when d=2mi:
Knowing that the plane flies at a constant speed of 500mi/h, we can calculate:
