A projectile is launched with an initial speed of Vo at an angle θ above the horizontal. It lands at the same level from which it was launched. What was the average velocity between launch and landing? Explain please because I can't understand this.
1 Answer
Explanation:
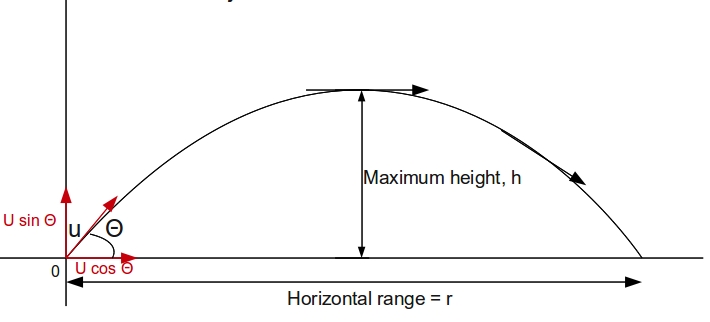
Typical flight of a projectile is as shown in the picture above.
In the problem it is given that initial velocity
This velocity can be resolved into its
Component along
Component along
We also know that both
Maximum height is achieved due to
This component of the velocity decreases due to action of gravity. Becomes zero at the maximum height point. Then increases due to gravity and becomes equal to initial
Let
It is given that "It lands at the same level from which it was launched", means that displacement in the
If we ignore air resistance,
Now to find the Resultant Average velocity we need to add both vectors along
Hence,
