Question

A rectangle is inscribed with its base on the x-axis and its upper corners on the parabola y=5-x^2. What are the dimensions of such a rectangle with the greatest possible area, rounded to the nearest 3 decimals?

Answer 1

Length: `2sqrt(5/3)`
Height: `10/3`
The maximum area is approximately `8.61` square units.

Explanation:

Let the two lower vertex of the rectangle be `(x, 0)` and `(-x, 0)`. This would mean that the length of the base would be `2x`. We can immediately see that the height will be `y`.

The area is therefore:

`A = 2xy`

But we want to eliminate one of these variables. We see that for the context of this problem, `y = 5 - x^2`. Thus:

`A = 2x(5 - x^2)`

`A = -2x^3 + 10x`

Now we differentiate to find the critical point(s).

`A' = -6x^2 + 10`

This will have critical point(s) when it equals `0`.

`0 = -6x^2 + 10`

`0 = -2(3x^2 - 5)`

`3x^2 = 5`

`x = +-sqrt(5/3)`

Therefore, the length will be `2sqrt(5/3)` and the height will be `5 - 5/3 = 10/3`

Hopefully this helps!

Answer 2

Maximum area of `8.607` occurs with dimension `2.582 xx 3.333`

Explanation:

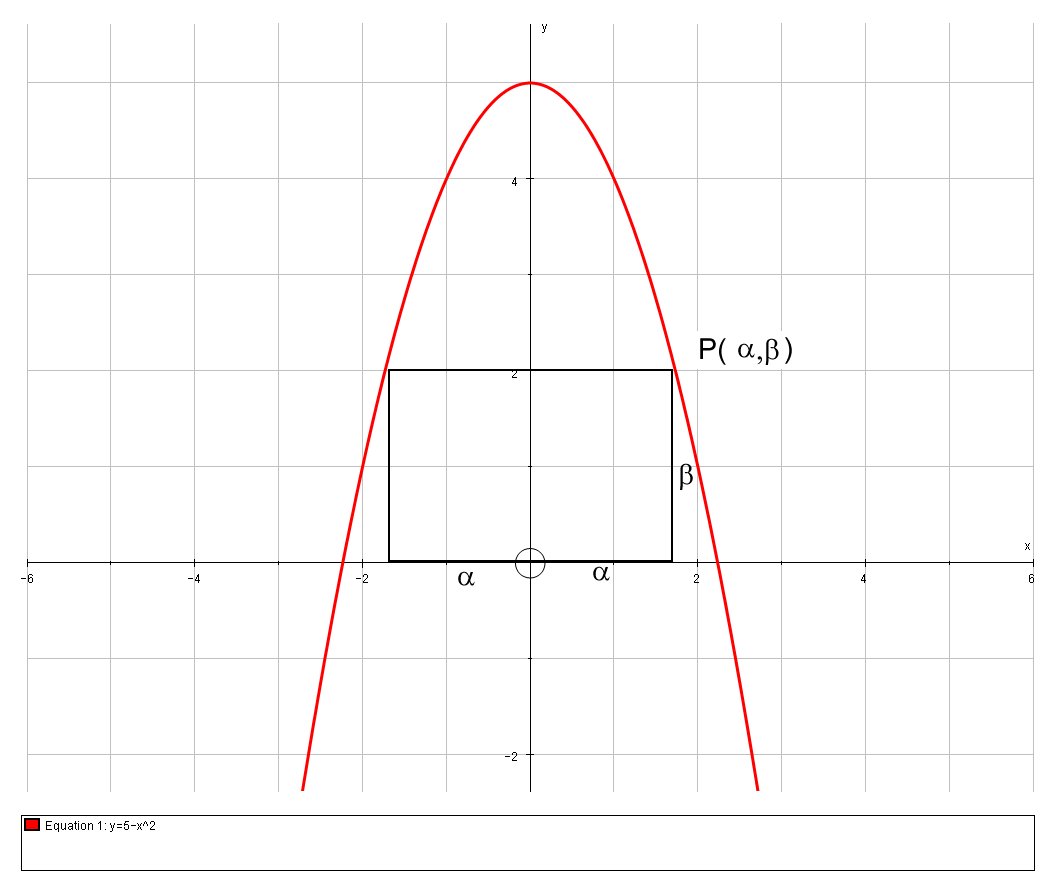
Let `P(alpha,beta)` be the top right hand coordinate of the rectangle that lies on the given parabola `y=5-x^2`, so that `alpha,beta gt 0`

Let us set up the following variables:

# { (alpha,"semi-width of rectangle"), (beta,"height of rectangle") (A,"Area of rectangle") :} #

Our aim is to find `A`, as a function of a single variable and to maximize the total area, `A` (It won't matter which variable we do this with as we will get the same result). ie we want a critical point of `A` wrt the variable.

As `P` lies on the curve `y=5-x^2`, we have:

`beta = 5-alpha^2 \ \ \ \ \ ..... [1]`

And the total Area is that of a rectangle of width `2alpha` and height `beta`, so:

`A = 2 alpha beta`
`\ \ \ = 2 alpha (5-alpha^2) \ \ \ \ \` (from [1] )
`\ \ \ = 10alpha-2alpha^3`

We now have the Area, `A`, as a function of a single variable `alpha`, so differentiating wrt `alpha` we get:

`(dA)/(d alpha) = 10-6alpha^2`

At a critical point we have `(dA)/(d alpha) =0 =>`

`10-6alpha^2 = 0`
`:. alpha^2 = 5/3 => alpha = +-sqrt(5/3)`

We require that `alpha gt 0 => alpha = sqrt(5/3) ~~ 1.2909944 ...`

With this value of `alpha` we have:

`beta = 5-alpha^2`
`\ \ = 5-5/3`
`\ \ = 10/3 ~~ 3.333333`

And the corresponding area is:

`A = 2 alpha beta`
`\ \ \ = 2 sqrt(5/3) 10/3 ~~ 8.6066296 ...`

We can visually verify that this corresponds to a maximum by looking at the graph of `y=A(alpha)`:
graph{10x-2x^3 [-2, 4, -5.5, 10]}

Which is consistent with a maximum of `~~8.6` when `alpah~~1.3`

Thus:
Maximum area of `8.607` occurs with dimension `2.582 xx 3.333`

Where the width is `2alpha`, height is `beta` and values are rounded to `3 \ dp`