A research assistant made 160 mg of radioactive sodium (Na^24) and found that there was only 20 mg left 45 h later, what is the half-life of Na^24?

Question

4554 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-04-12T13:10:18

The half life is #=15h#

There are 2 ways for solving this problem

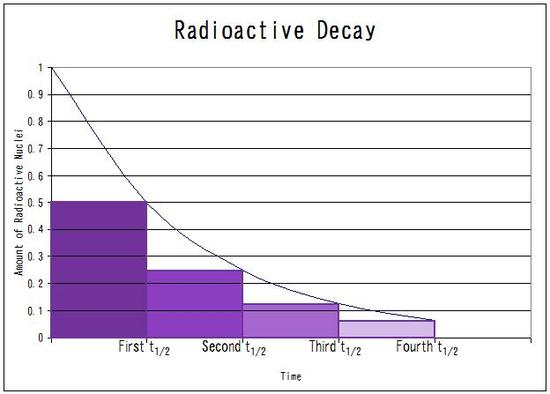
enter image source here

Every half life, the amount is divided by #2#

After #1*t_(1/2)#, the amount left is #160/2=80#

After #2*t_(1/2)#, the amount left is #80/2=40#

After #3*t_(1/2)#, the amount left is #40/2=20#

The half life is

#t_(1/2)=45/3=15h#

The half life of sodium 24 is #t_(1/2)#

The radioactive decay constant is #lambda=ln2/(t_(1/2))#

We apply the equation

#A=A_0*e^(-lamdat)#

The activity is proportional to the mass.

#m=m_0*e^(-lamdat)#

#160=20*e^-(ln2/t_(1/2)*45)#

#8=e^-(ln2/t_(1/2)*45)#

#(ln2/t_(1/2)*45)=ln8#

#t_(1/2)=ln2/ln8*45#

#=ln2/(3ln2)*45#

#=15h#