A right triangle has sides A, B, and C. Side A is the hypotenuse and side B is also a side of a rectangle. Sides A, C, and the side of the rectangle adjacent to side B have lengths of #7 #, #6 #, and #15 #, respectively. What is the rectangle's area?
1 Answer
Feb 18, 2016
Explanation:
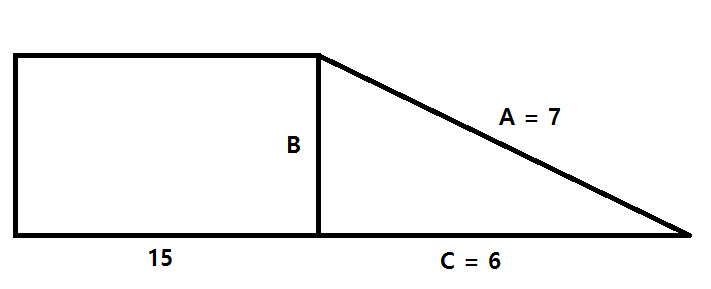
The above (not to scale) picture contains the information given in the problem. In many geometry problems, drawing a picture is a good way to start.
The area of the rectangle is the product of the lengths of its sides, in this case
Substituting in the given values for
Thus the area of the rectangle is

