A right triangle has sides A, B, and C. Side A is the hypotenuse and side B is also a side of a rectangle. Sides A, C, and the side of the rectangle adjacent to side B have lengths of #8 #, #7 #, and #14 #, respectively. What is the rectangle's area?
1 Answer
Explanation:
Draw the diagram
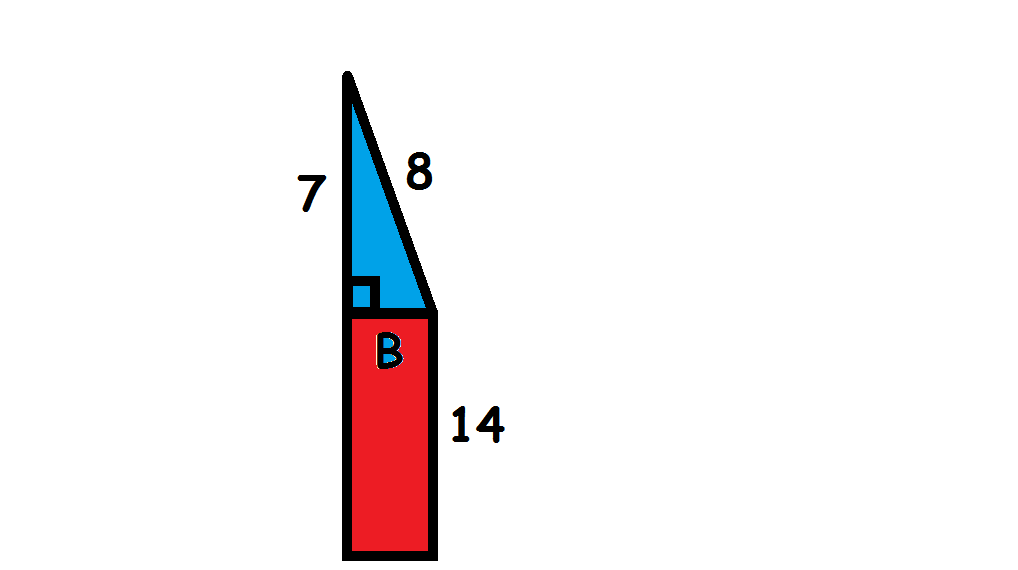
To find the are of the triangle at the bottom,
We need to find the length of
As the triangle is a right angle triangle,
We use the
#color(blue)(a^2+b^2=c^2#
Where,
#color(orange)("c = Longest side (hypotenuse)"#
#color(orange)("a and b are the other sides"#
So,
#color(purple)(c=8#
#color(purple)(b="B"#
#color(purple)(a=7#
Insert the following (above) in the formula
Take the square root of both sides
Let's redraw the diagram
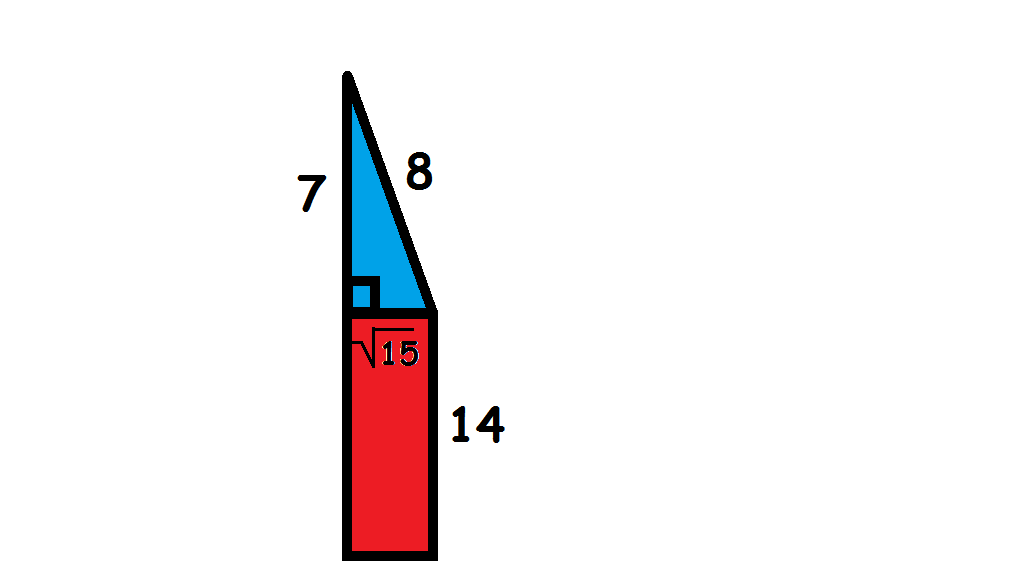
Now, we need to find the area of the rectangle
We use the formula
#color(brown)("Area of rectangle"=l*b#
Where,
#color(orange)(l="length"=14#
#color(orange)(b="breadth"=sqrt15#

