A right triangle has sides A, B, and C. Side A is the hypotenuse and side B is also a side of a rectangle. Sides A, C, and the side of the rectangle adjacent to side B have lengths of #7 #, #4 #, and #1 #, respectively. What is the rectangle's area?
1 Answer
Aug 15, 2017
The rectangle's area is
Explanation:
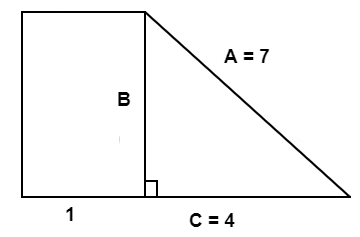
Above is a drawing of the situation in question.
Since we have two sides of a right triangle, we can use the Pythagorean theorem to calculate the length of side B.
Be sure to note that a and b here refer to the smaller sides of the triangle and the c refers to hypotenuse, which is different from the letters in our diagram!
Now, to calculate the area of the rectangle, we must multiple its length by its width. Side B is its length and we already know its width is 1, and since any number multiple by 1 is just itself, the area of the rectangle is

