A right triangle has sides A, B, and C. Side A is the hypotenuse and side B is also a side of a rectangle. Sides A, C, and the side of the rectangle adjacent to side B have lengths of #13 #, #4 #, and #3 #, respectively. What is the rectangle's area?
1 Answer
Apr 11, 2016
Explanation:
Consider the diagram
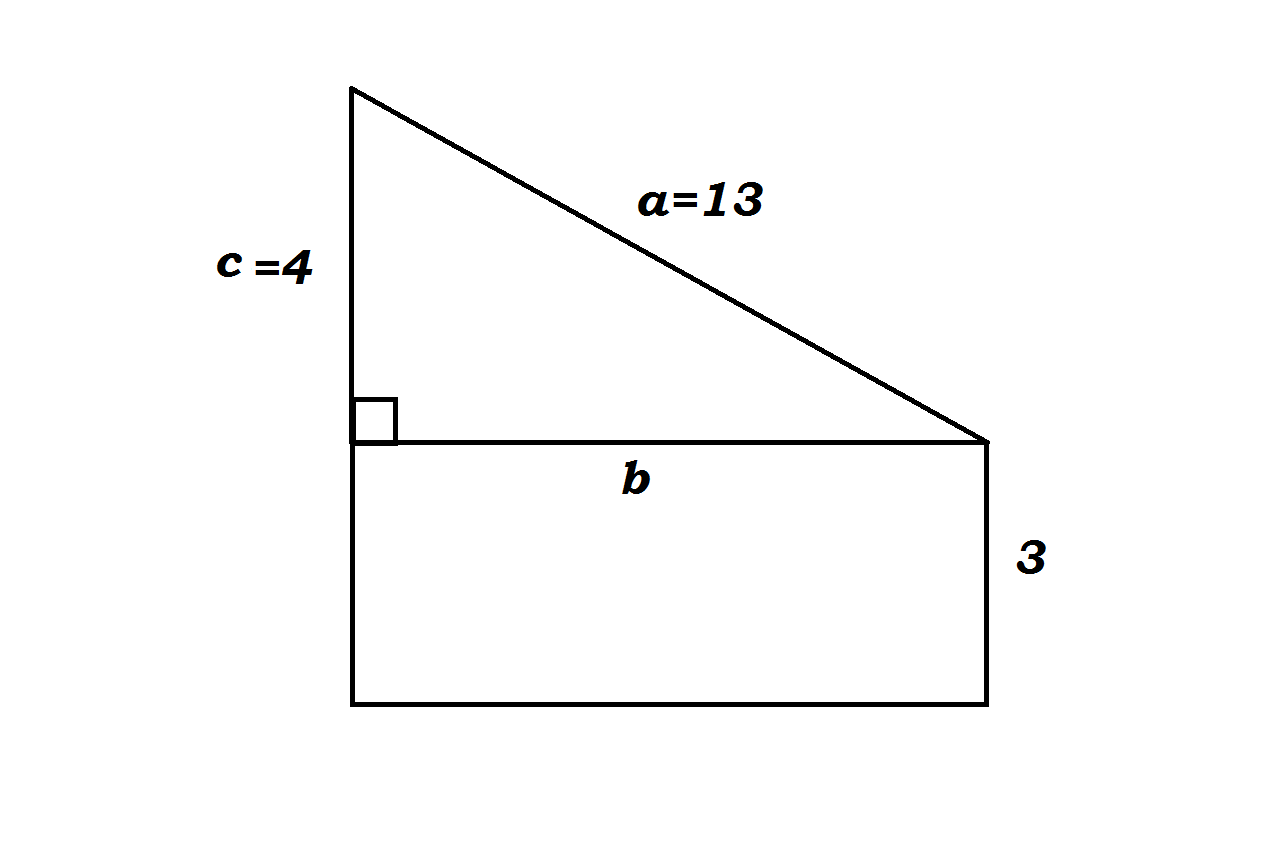
We can find the length of
#color(blue)(a^2+b^2=c^2#
Where,
#aand b# are the right-containing sides and#c# is the Hypotenuse (longest side of a right-triangle)
But,
In this case,
So,
Now we need to find the area of the rectangle
Area=
Where,
#l=l# #eng# #th,b=breadth#
#color(violet)(l=3sqrt17,b=3#

