Question

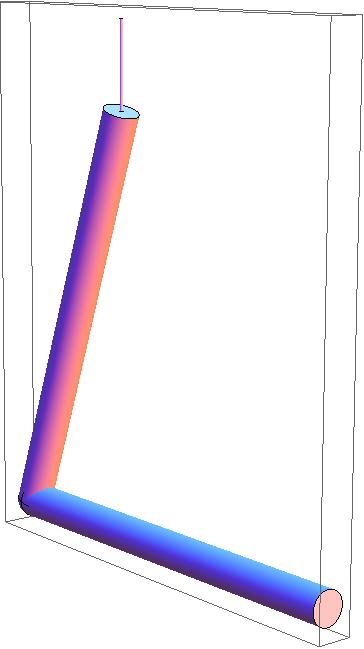
A rigid body in the shape of a 'V' has two equal arms made of uniform rods. What must be the angle between the two rods so that when the body is suspended from one end, the other end is horizontal?

Thank you!

Answer 1

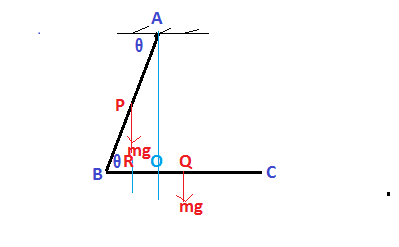
Let two uniform rods each of mass m and length l joined at angle `theta` constitute the V shaped rigid body ABC. The rigid body is suspended freely from point A and its BC part becomes horizontal and AB part remains inclined at angle `theta` with the horizontal when the system comes in equilibrium.

Let the midpoint of AB be P and that of BC be Q.The vertical line drawn through the point of suspension A intersects BC rod at O.The weight of AB part `mg` will act vertically downward through P and its line of action intersects BC at R. Again weight (mg) of BC will act downward through its mid point Q .These two weights will lie in two opposite sides of O

The perpendicular distannce of the weight acting through P from O is `OR=l/2costheta`.
Again the perpendicular distance of the weight acting through Q from O is

`OQ=BQ-BO=l/2-lcostheta`

So at equlibrium of two weigts

`mgxxOR=mgxxOQ`

`mgxxl/2costheta=mgxx(l/2-lcostheta)`

`=>3/2costheta=1/2`

`=>costheta=1/3`

`=>theta=cos^-1(1/3)= 70.5^@`

Answer 2

`theta=2arccos(sqrt(2/3))approx70.53^@`

Explanation:

Let `A,B,C` denote the rigid body geometry, with `bar(AC)` a rod, `bar(BC)` the other rod, joined at vertex `C`.

The rigid body baricenter is found as the baricenter of the rod's baricenters. So

`G = ((A-C)/2+(B-C)/2)/2 = (A+B)/4-C/2`

Calling `hat(ACB)=theta` we have

`abs(bar(CG))=abs(bar(AC))cos(theta/2)`

This baricenter pertains to the vertical issuing from the hanging point.

Supposing that the rigid body is suspended by the point `A` then in equilibrium, the rod `bar(BC)` must be horizontal. We know also that `G` is located into the bissectrice of `hat(ACB)=theta` then if `phi` is the angle between `bar(AC)` and the vertical, we have

`sin(phi)=abs(bar(CG))cos(theta/2)/abs(bar(AC))`

but `phi+theta=pi/2` so

`cos(theta)=abs(bar(CG))/abs(bar(AC))cos(theta/2)`

but `abs(bar(CG))=abs(bar(AC))/2cos(theta/2)` so remains

`cos(theta)=1/2cos^2(theta/2)`

but

`cos(theta)=2cos^2(theta/2)-1`

then

`cos(theta/2)=sqrt(2/3)`

so

`theta=2arccos(sqrt(2/3))approx70.53^@`