A rock is dropped from rest from the roof of a building 100 m high. What is the velocity of the rock at the moment it reaches the ground? How long does it take to hit the ground?
2 Answers
The final velocity of the rock is
Explanation:
There are at least two ways to solve this, one being with kinematics and the other with a combination of kinematics and energy conservation. These are just the first two that come to mind. I'll give an explanation of both methods.
Method 1: Kinematics
This is a projectile motion problem which can be solved using kinematics. Because the rock is dropped from rest, we know its initial velocity is
We can use this kinematic equation to solve for the final velocity,
where
Using our known values:
To find the fall time, we can use this kinematic equation:
Because
You could also use
Method 2: Energy Conservation/Kinematics
Where
Kinetic energy is given by
As the rock is not moving initially (i.e. at rest), for our intents and purposes it possesses only gravitational potential energy. When it is dropped, that gravitational potential energy is transformed into kinetic potential energy as it falls. Just before the rock hits the ground, it has only kinetic energy (
We can see that mass cancels, as it is present on both sides, giving:
Solving for
You would then take that final velocity and use a kinematic equation to find Δt, either the one used above in the kinematics method or
Hope that helps!
The final velocity is
The rock will take
Explanation:
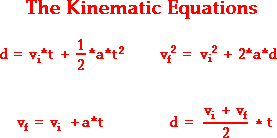
To find the final velocity, use the kinematic equation
Substitute the given values into the equation.
To determine the length of time it takes for the rock to fall, use the kinematic equation
Rearrange the equation to isolate


