A sample of air has a volume of 140.0 mL at 67°C . At what temperature will its volume be 50.0 mL at constant pressure?
1 Answer
Explanation:
Volume and temperature have a direct relationship when pressure and number of moles are kept constant - this is known as Charles' Law.
What that means is that when pressure and number of moles are kept constant, increasing the temperature will result in an increase in volume.
Likewise, a decrease in temperature will result in a decrease in volume.
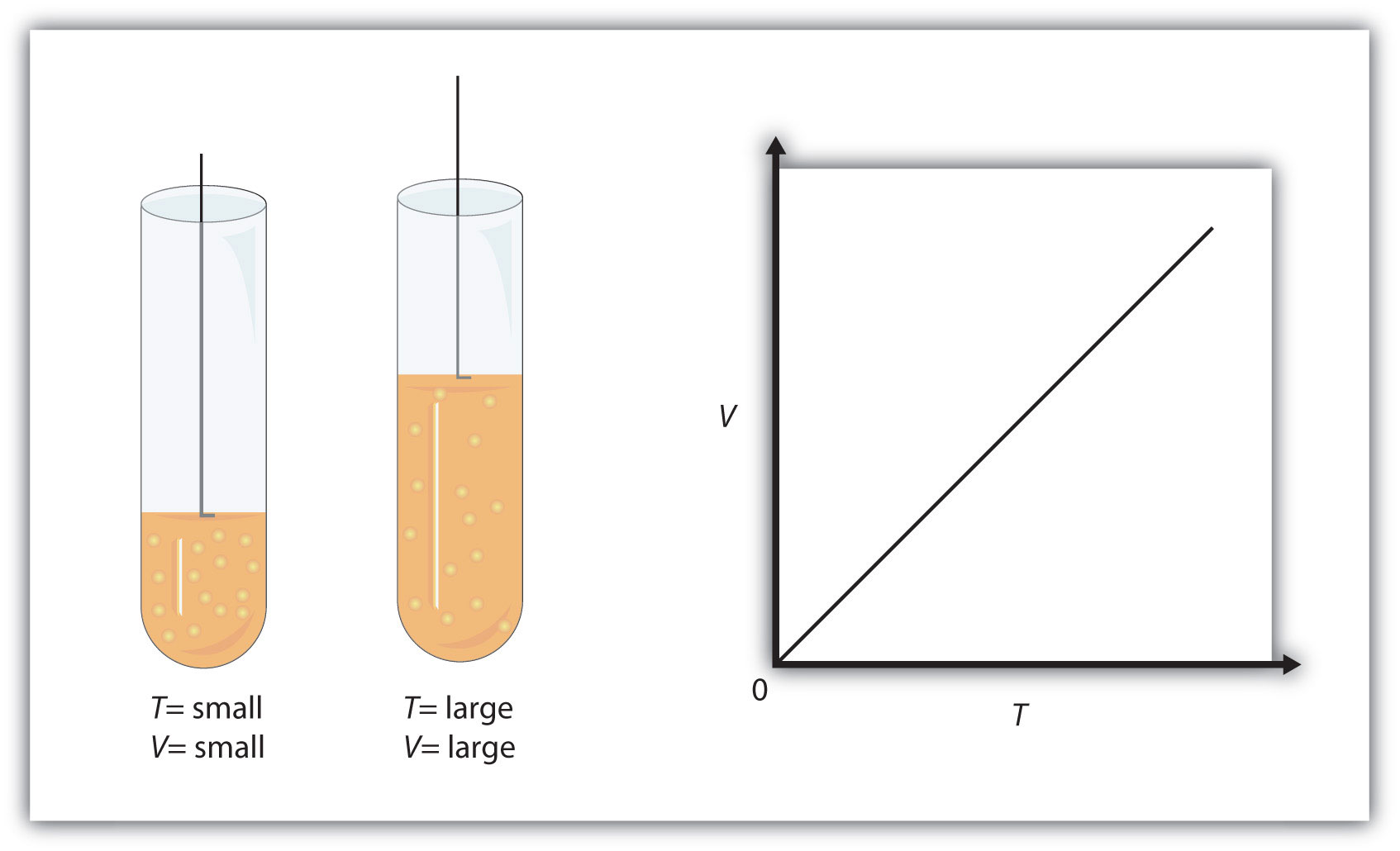
In your case, the volume of the gas decreased by a factor of about
Mathematically, this can be written as
#color(blue)(V_1/T_1 = V_2/T_2)" "# , where
It is important to remember that the temperature of the gas must be expressed in Kelvin. The initial temperature of the gas will be
#T_1 = (273.15 + 67.0)"K" = "340.15 K"#
Rearrange the above equation to solve for
#V_1/T_1 = V_2/T_2 implies T_2 = V_2/V_1 * T_1#
#T_2 = (50.0 color(red)(cancel(color(black)("mL"))))/(140.0color(red)(cancel(color(black)("mL")))) * "340.15 K"#
#T_2 = "121.48 K"#
Rounded to three sig figs, the answer will be
#T_2 = color(green)("121 K")#
If you want, you can express this in degrees Celsius
#T_2 = 121 - 273.15 = -152^@"C"#

