A satellite orbits the Earth at a height of 100km above the surface, at a velocity of 7,850m/s. How many hours does it take to complete 1 revolution around the Earth?

1 Answer
Gió
Dec 24, 2014

We have the following situation:
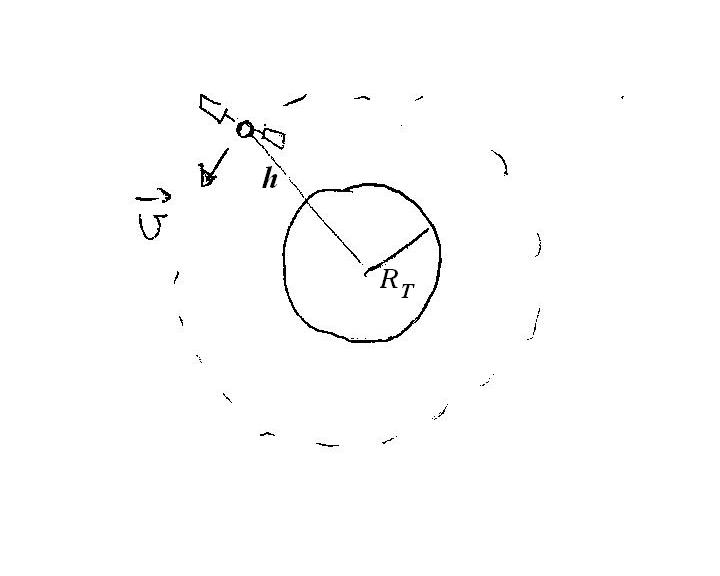
enter image source here
Where:
Earth radius: #R_T=6,371 km#
Eight of satellite: #h=100 km#
Velocity of satellite: #|vecv|=v=7,850 m/s#

The distance that the satellite must cover in one revolution is equal to the circumference: #2pir=2pi(R_T+h)#
The time needed to do that is: #t=(2pi(R_T+h))/v#

Remember thar: #(R_T+h)=6,371+100=6,471 km=6,471*10^3 m#
and:
#t=2pi(R_T+h)/v=(2pi*6,471*10^3)/(7,850)=5,179 s~~1h 26min 19s#

Related questions
See all questions in Circular Motion
Impact of this question
6827 views around the world
You can reuse this answer
Creative Commons License