A segment has a midpoint (-2, 9) and one endpoint (2,8). What is the coordinate of the other endpoint?
2 Answers
See a solution process below:
Explanation:
The formula to find the mid-point of a line segment give the two end points is:
Where
Subtituting gives:
Solving for
Solving for
The other end point is:
The coordinate of the other endpoint is
Explanation:
Instead of full-on visualizing a graph, let's start with a number line:
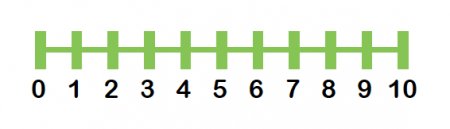
This is a simple number line from
Let's try it with two more numbers. How about
Now we can see that there's a formula that we can use to calculate the midpoint between any two numbers! Add the two end numbers up and divide the result by
For any two endpoints
So how does all of this relate to the problem? Well, remember that the graph is a coordinate plane, made up of two axes - the x-axis and the y-axis. And you can think of each axis to be a number line!
So now, our task is to derive a formula for finding the midpoint between any two points on the coordinate point. That way, we can write a relationship between the two endpoints on the coordinate plane and the midpoint between those two points.
Suppose there was a graph like the one shown below:
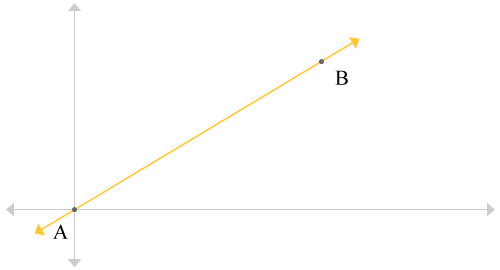
Suppose point A had the coordinates
Let's focus on the x-axis first and treat it as a number line, except without numbers. On the x-axis, we have the x-coordinate of point A as well as the x-coordinate of point B. From our earlier rule, we can state that the midpoint between the two x-coordinates is:
Likewise, the midpoint between the two y-coordinates is:
As we stated earlier, the coordinates of the midpoint between points A and B are the midpoint between the two x-coordinates and the midpoint between the two y-coordinates. Combining the two statements above, we get the conclusion that the coordinates of the midpoint between points A and B are:
Now, with that information, we can substitute in the values mentioned in the question. We let point A and its coordinates be our missing endpoint, point B and its coordinates be our known endpoint, and point M, our midpoint, and its coordinates be the midpoint, like so:
This equation tells us that
Let's start with the left equation:
And now, let's solve the right equation:
And now, we put the two values together to form the answer:


