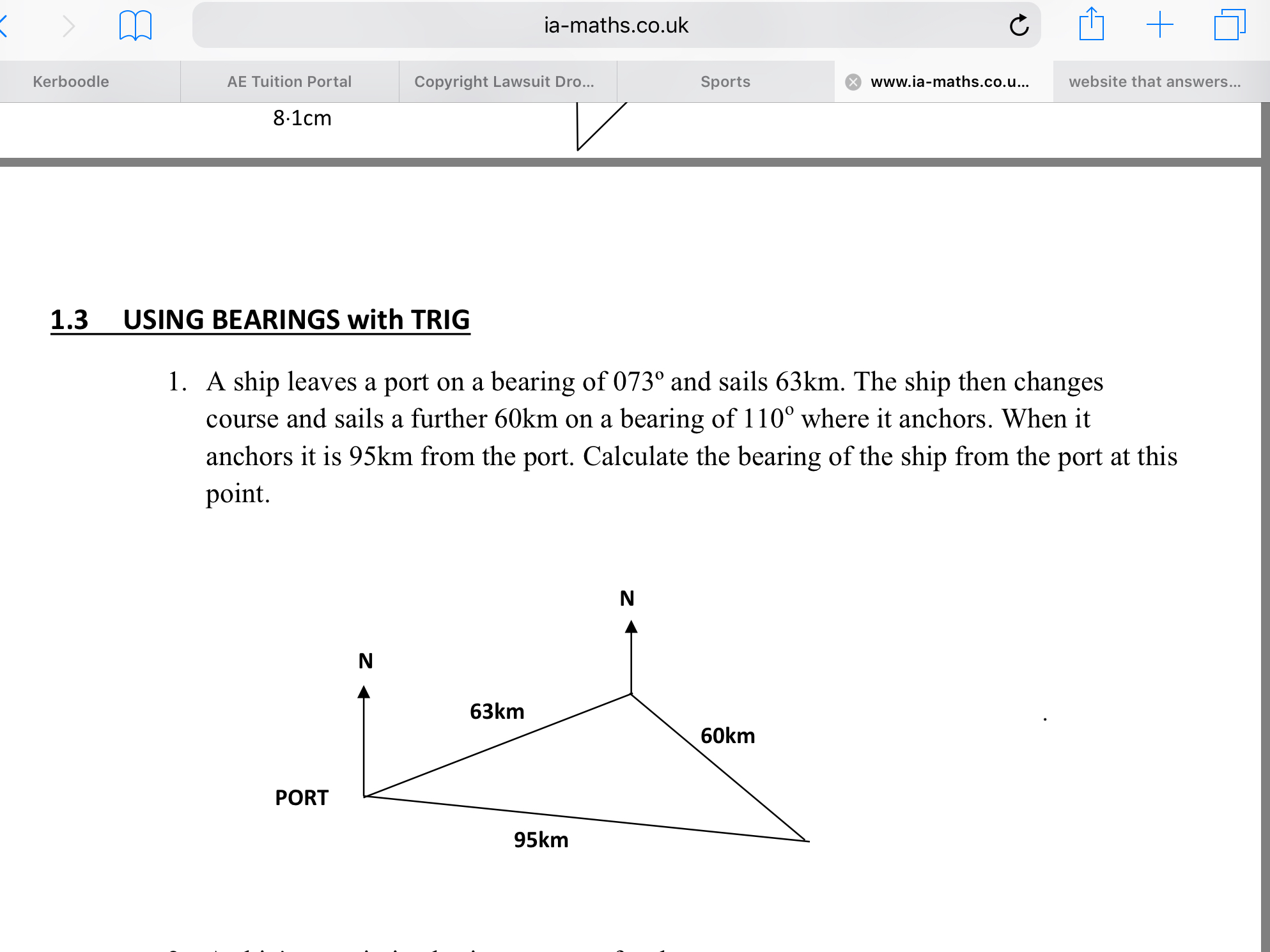
A ship leaves a port on a bearing of 073° and sails 63km. The ship then changes course and sails a further 60km on a bearing of 110° where it anchors. When it anchors it is 95km from the port. Calculate the bearing of the ship from the port at this point?
2 Answers
About
Explanation:
The bearing is the angle measured clockwise from true north.
It will be
The problem seems overdetermined, meaning there are several different ways to get the answer that might not give the same result. We'll use the Law of Cosines:
Bearing of
The problem is inconsistent; adding the vectors we get about
Explanation:
Here's a solution that doesn't use the Law of Cosines.
Let's put this on the Cartesian Grid with the port being the origin
Bearings are complementary to the usual angles we consider with the x axis, so a bearing of
But we don't have to think about it that way; sine and cosine kinda reverse when we do things relative to the y axis, but it's not that complicated.
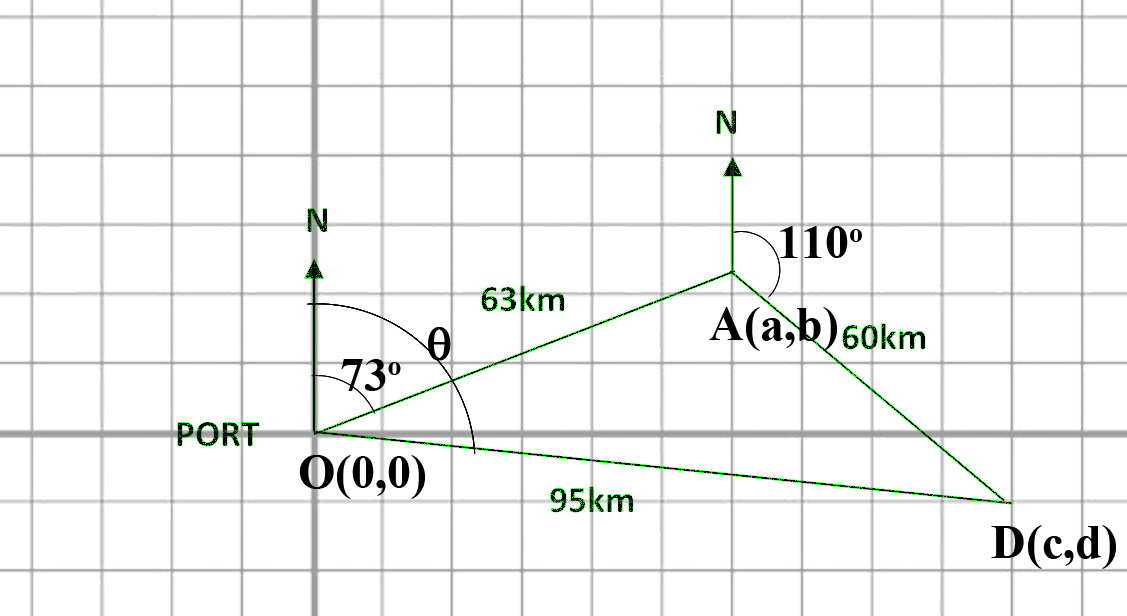
Let's call the spot after the first leg, 63 km, point
The points
It's switched from normal because we're using bearings.
If
That's inconsistent with the answer determine by the Law of Cosines, either because I made a mistake or the person who wrote the question made a mistake. It's also inconsistent with
Let's see if we can figure out which. Alpha knows.

Note it says edge lengths 63, 60, 116.648. Compare that to
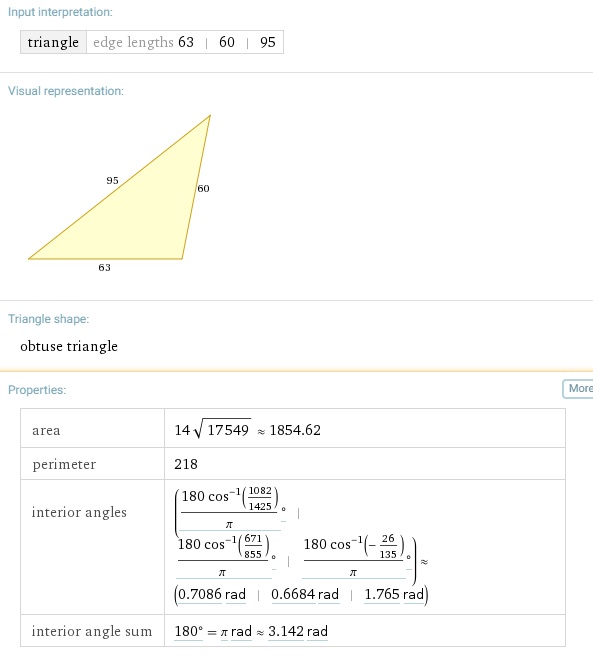
Those are not the same triangles but it looks like my math is OK.
Angle A is
Looks like a bad problem.

