The Law of Cosines
Key Questions
-
The Law of Cosine can only be used if two sides and their enclosed angle are known.
In all other cases the Law of Sines has to be used.
-
Yes, the Law of Cosines works for all triangles.
However, the proof depends on the shape a triangle, more precisely, how an altitude from some vertex falls onto the opposite side.
For example, consider a triangle
#Delta ABC# with vertices#A# ,#B# and#C# , corresponding angles#alpha# ,#beta# and#gamma# and correspondingly opposite sides#a# ,#b# and#c# .
Let's prove the Law of Cosines that states:
#a^2+b^2-2*a*b*cos(gamma) = c^2# Let's draw altitude
#AH# from vertex#A# to an opposite side#BC# with an intersection of this altitude and a side#BC# at point#H# .
There are different cases of a location of point#H# relatively to vertices#B# and#C# .
It can lie in between vertices#B# and#C# .
It can lie outside of#BC# on a continuation of this side beyond vertex#B# or beyond vertex#C# .Assume that a base of this altitude, point
#H# , is lying on the continuation of#BC# beyond a point#C# (so,#C# is in between#B# and#H# ) and prove the Law of Cosines in this case. Other cases are similar to this one.Let's use the following symbols for segments involved:
#AH# is#h#
#BH# is#a_1#
#CH# is#a_2#
Then, since#C# lies in between#B# and#H# ,
#a = a_1 - a_2# or#a_1=a+a_2#
Since both#Delta ABH# and#Delta ACH# are right triangles, by trigonometric dependency between hypotenuse, catheti and angles and by Pythagorean Theorem
#h = b*sin(pi-gamma) = b*sin(gamma)#
#a_2 = b*cos(pi-gamma) = -b*cos(gamma)#
#c^2 = h^2+a_1^2 = b^2*sin^2(gamma)+(a-b*cos(y))^2 =#
#=b^2*sin^2(gamma)+a^2-2*a*b*cos(gamma)+b^2*cos^2(gamma)=#
#=a^2+b^2(sin^2(gamma)+cos^2(gamma))-2*a*b*cos(gamma)=#
#=a^2+b^2-2*a*b*cos(gamma)# End of Proof
When point
#H# lies in between vertices#B# and#C# or on a continuation of side#BC# beyond vertex B, the proof is similar.See Unizor Trigonometry - Simple Identities - Law of Cosines for visual presentation and more detailed information.
-
Answer:
#cos(gamma)=(a^2+b^2-c^2)/(2ab)# Explanation:
We have
#c^2=a^2+b^2-2abcos(gamma)#
so
#2abcos(gamma)=a^2+b^2-c^2#
Isolating#cos(gamma)#
#cos(gamma)=(a^2+b^2-c^2)/(2ab)# -
Cosider the triangle:
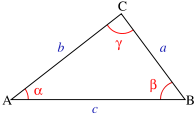
(Picture source: Wikipedia)you can relate the sides of this triangle in a kind of "extended" form of Pitagora's Theorem giving:
#a^2=b^2+c^2-2bc*cos(alpha)#
#b^2=a^2+c^2-2ac*cos(beta)#
#c^2=a^2+b^2-2ab*cos(gamma)# As you can see you use this law when your triangle is not a right-angled one.
Example:
Consider the above triangle in which:
#a=8 cm#
#c=10 cm#
#beta=60°# therefore:
#b^2=a^2+c^2-2ac*cos(beta)#
#b^2=8^2+10^2-2*8*10*cos(60°)# but#cos(60°)=1/2#
so:#b^2=84 and b=sqrt(84)= 9,2 cm#