Question

A spherical ball of radius r and relative density 0.5 is floating in equilibrium with half of it immersed in water. The work done in pushing the ball down so that whole of it just immersed in water is? [`rho` is the density of water].

Answer 1

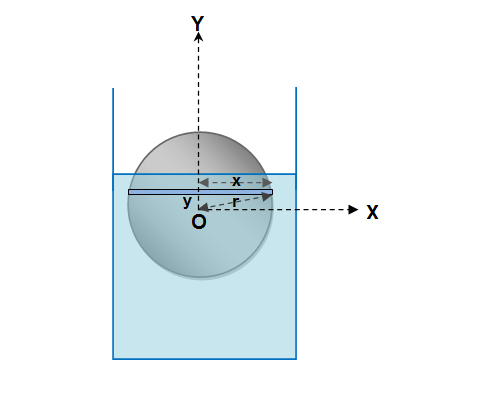
At equilibrium position the sphere floats with half of its volume `V/2` immersed in water,where V represents the volume of the spherical ball under consideration. Given that the density of the material of the sphere is `d=0.5` and that of water is `rho` then by applying condition of floatation we can write

`Vdg=1/2Vrhog` ,where `g` is the acceleration due to gravity.

Hence `rho=2d=2xx0.5=1`

Now considering the situation when the sphere is pushed to some depth in the water from its equilibrium position. For the sake of calculation applying integral calculus we consider X-axis and Y-axis as shown in figure and a very thin disk element of displaced water of thickness `dy` and of radius `x` at a distance `y` from origin in the immersed portion of the sphere. Here center of the sphere is taken as origin.
The upward buoyant due to displaced water of thin disk element considered will be given by

`dF=rhogpix^2dy=pirhog(r^2-y^2)dy`

So the variable buoyant force, a function of `y` acting on the sphere due to immersion of depth `y` from equilibrium position will be given by

`F(y)=int_0^ypirhog(r^2-y^2)dy=pirhog[r^2y-y^3/3]`

So the work done against the variable buoyant force due to immersion of the sphere to the `r` depth from its equilibrium position will be given by

`W=int_0^rF(y)dy=int_0^rpirhog[r^2y-y^3/3]dy`

`=pirhog[r^2y^2/2-y^4/12]_0^r=pirhog(r^4/2-r^4/12)`

`=5/12pir^4rhog=5/12pir^4g` (putting `rho=1)`

Alternative way

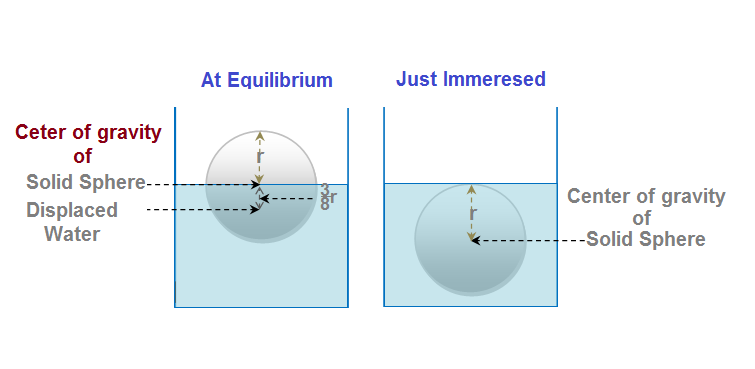
The above figure represents the two positions of the sphere as described in the problem. We can solve the problem considering the potential energy change of the sphere and its displaced water in two positions of the sphere.

Now it is given that the radius of the spherical ball `=r`

So its volume `V=4/3pir^3`

At floating equilibrium condition the center of gravity of the sphere is at the level of water and when it is just immersed by pushing its center of gravity is shifted downward by a distance of `r` as evident from the figure.

Hence the decrease in PE of the sphere due to this shift will be given by `DeltaU_"sphere"=Vdgr=Vxx0.5gr=1/2Vgr`

Again at floating equilibrium state of the sphere the center of gravity of the hemispherical displaced water (or the center of bouncy ) is at the depth of `3/8r` * from the level of water and in its just immersed condition it rises to the level of water.

Here the gain in PE of displaced water will be
`Delta U_"displaced water"=V/2rhogxx3/8r=3/16Vgr` [since `rho=1`]

Considering that there exists no initial and final KE . Then we can say that the work done `W` in pushing the ball down is nothing but the net energy change of the process.

So `W=DeltaU_"sphere"-DeltaU_"displaced water"`

`=>W=1/2Vgr-3/16Vgr==(1/2-3/16)Vgr=5/16Vgr`

`=>W=5/16xx4/3pir^3gr` `" "[color(red)("Inserting "V=4/3pir^3)]`

`=>W=5/12pir^4g`

• Please note
  To understand position of CG of a solid hemisphere please click