Question

A spherical shell of radius `R` and uniformly charged with charge `Q` is rotating about its axis with frequency `f`. Find the magnetic moment of the sphere?

Answer 1

Uniformly charged spherical shell of radius `R` carries a total charge `=Q`
Hence it has surface charge density

`sigma=Q/(4πR^2)`

It rotates about its axis with frequency`=f`
`:.` Its angular velocity `omega=2pif`
Suppose the angular velocity `vecomega=omegahatz`

To find the magnetic moment of spinning shell we can divide
it into infinitesimal charges.
Using spherical polar coordinates `(rho, phi, theta)` with origin at the center of the spherical shell, we consider infinitesimal area `dS` of a circular ring of infinitesimal width and of radius `r` located at a distance `R` from the origin on the surface of sphere.
Here `vecr=Rsinthetahatr` and coordinate `rho=R`, is constant for each elemental area.

`dq=sigmadS=sigmaR^2sinthetad thetadphi`

Current in the ring is given by

`dI=(dq)xxf=(sigmaR^2sinthetad thetadphi)xxomega/(2pi)`
`=>dI=(omegasigmaR^2sinthetad thetadphi)/(2pi)`

Now the magnetic dipole moment of ring is given by the expression in terms of position vector `vecr` and current density `vecJ` as

`dvecm=1/2int_"ring"vecrxxvecJ`
`=>dvecm=1/2dIint_"ring"vecrxxdvecl`
where `dvecl` is element length of the ring.

Line integral becomes equal to the circumference of ring`=2piRsintheta`

`:.dvecm=dI(piR^2sin^2theta)hatz`

Inserting value of `dI` we get

`dvecm=(omegasigmaR^2sinthetad thetadphi)/(2pi)(piR^2sin^2theta)hatz`
`=>dvecm=(vecomegasigmaR^4sin^3thetad thetadphi)/2`

Total magnetic moment is integral with respect to both variables within respective limits

`vecm=(vecomegasigmaR^4)/2int_0^pisin^3thetad thetaint_0^(2pi)dphi`
`=>vecm=(vecomegasigmaR^4)/2xx4/3xx2pi`
`=>vecm=4/3pisigmaR^4vecomega`

Rewriting in terms of charge `Q`

`vecm=4/3pi(Q/(4πR^2))R^4vecomega`
`vecm=Q/3R^2vecomega`

.-.-.-.-.-.-.-.-

Reference figure for `dS`

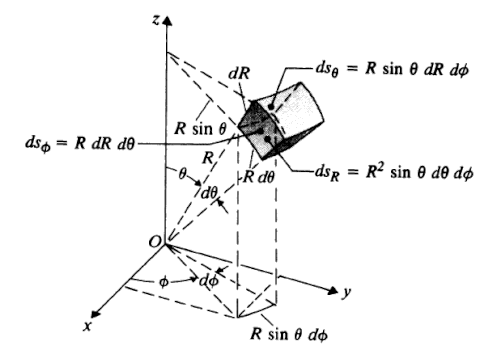
Using online integral calculator

`int_0^pisin^3thetad theta=|cos^3theta/3-costheta|_0^pi=4/3`