A spring with a constant of #9# #kgs^-2# is lying on the ground with one end attached to a wall. An object with a mass of #2# #kg# and speed of #12# #ms^-1# collides with and compresses the spring until it stops moving. How much will the spring compress?
2 Answers
Jun 11, 2017
The compression is
Explanation:
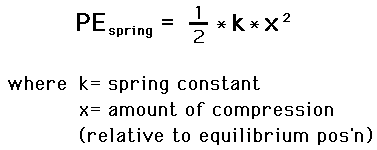
The spring constant is
The kinetic energy of the object is
This kinetic energy will be stored in the spring as potential energy.
So,
Jun 11, 2017
The displacement of the spring,
Explanation:
The kinetic energy of the moving object will be
This will be converted to spring potential energy:
Rearranging:
We can substitute in the calculated value of

