Question

A stone of mass 1 kg is tied to the end of a string of length 5 metre and whirled in a vertical circle . What will be the minimum speed required at the lowest position to complete the circle?

Answer 1

`15.66 m/s`

Explanation:

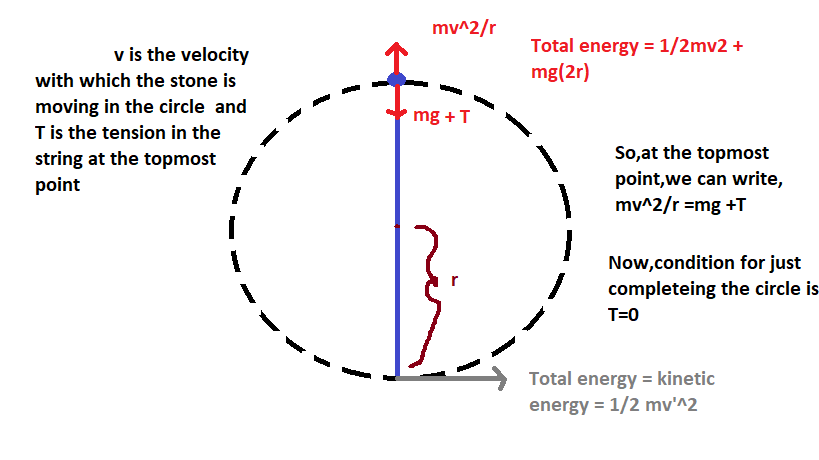
For the stone to just complete a vertical circle, tension in the string will be zero,so that its weight will be enough to supply the required centripetal force for the completion of the circle.

So, `(mv^2)/r =mg` (`v` is the velocity at the topmost point,and `r` = string length = `5m`)

or, `v = sqrt(rg) = sqrt(5*9.81)=7 m/s`

Now,if the velocity at the lowest point be `v'` , applying law of conservation of energy we can say, total energy at the topmost point =total energy at the lowest point.

i.e `1/2 mv^2 + mg (2r) = 1/2 mv'^2` (`mg2r` is the potential energy gained due to rising by height `r+r=2r`)

So,putting the values we get, `v'= sqrt(5gr)=15.66 m/s`