A superhero launches himself from the top of a building with a velocity of 7.3m/s at an angle of 25 above the horizontal. If the building is 17 m high, how far will he travel horizontally before reaching the ground? What is his final velocity?
2 Answers
A diagram of this would look like this:
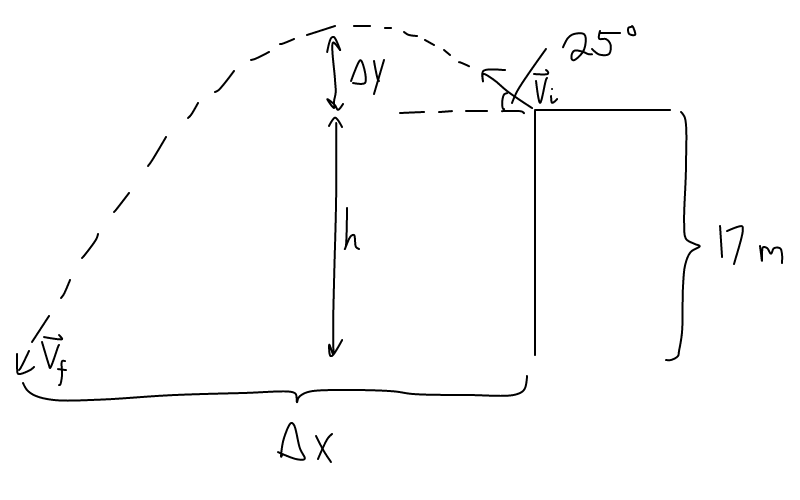
What I would do is list what I know. We will take negative as down and left as positive.
h = "17 m"h=17 m
vecv_i = "7.3 m/s"→vi=7.3 m/s
veca_x = 0→ax=0
vecg = -"9.8 m/s"^2→g=−9.8 m/s2
Deltavecy = ?
Deltavecx = ?
vecv_f = ?
PART ONE: THE ASCENSION
What I would do is find where the apex is to determine
One equation involving
\mathbf(vecv_(fy)^2 = vecv_(iy)^2 + 2vecgDeltavecy) where we say
vecv_(fy) = 0 at the apex.
Since
For part 1:
color(blue)(Deltavecy) = (vecv_(fy)^2 - v_(iy)^2)/(2g) = color(blue)((-v_(iy)^2)/(2g)) > 0 where
vecv_(fy) = 0 is the final velocity for part 1.
Recall that a vertical velocity has a
color(green)(Deltavecy = (-v_(i)^2 sin^2theta)/(2g)) > 0
Now that we have
The total height of the fall is
I get
PART TWO: THE FREE FALL
We can again treat the
At the apex, recall that
\mathbf(h + Deltavecy = 1/2g t_"freefall"^2) + cancel(v_(iy)t_"freefall")^(0)
Now we can just solve for the time it takes to hit the ground from the apex.
color(green)(t_"freefall") = sqrt((2(h + Deltavecy))/g)
= color(green)(sqrt((2(h - (v_(i)^2 sin^2theta)/(2g)))/g)) and of course, time is obviously not ever negative, so we can ignore the negative answer.
...And we're getting there.
PART THREE: SOLVING FOR THE HORIZONTAL DISTANCE
We can reuse the same kinematics equation as the one previously examined. One of the things we have been going for is
color(blue)(Deltax) = cancel(1/2a_xt^2)^(0) + v_(ix)t
And like before, use a trig relation to get the
= color(blue)(vecv_icostheta*t_"overall") > 0 where
t_"overall" is NOT what we got in part 2, but will include the timet_"leap" going from the building to the apex of the flight andt_"freefall" that we acquired earlier.
Deltay = 1/2vecg t_"leap"^2 + vecv_(iy)t_"leap"
With
t_"leap" = (-(vecv_(iy)) + sqrt((vecv_(iy))^2 - 4(1/2vecg)(-|Deltay|)))/(2*1/2vecg)
~~ "0.3145 s"
Include the time acquired for apex to the ground and you should get about
t_"overall" = t_"leap" + t_"freefall"
Using
PART FOUR: SOLVING FOR THE FINAL VELOCITY
Now this is going to require a bit more thinking. We know that
tantheta' = (h+Deltavecy)/(Deltavecx)
color(blue)(theta' = arctan((h+Deltavecy)/(Deltavecx)))
Notice how we used
And finally, since
color(green)(vecv_(fx)) = vecv_(ix) = vecv_fcostheta' = color(green)(vecv_icostheta') > 0
where
vecv_(fy)^2 = cancel(vecv_(iy)^2)^(0) + 2vecg*(h+Deltavecy)
Hence, this becomes:
color(green)(vecv_(fy) = -sqrt(2vecg*(h+Deltavecy))) < 0
Remember that we defined down as negative, so
Okay, we're ALMOST there. We are asked for
vecv_f^2 = vecv_(fx)^2 + vecv_(fy)^2
color(blue)(vecv_f = -sqrt(vecv_(fx)^2 + vecv_(fy)^2)) < 0
Overall,
And that would be all of it! Check your answer and tell me if it worked out.
Here the vel. of projection,
the angle. of projection ,
The upward vertical component of vel of projection ,
The building being 17m high , the net vertical displacement reaching the ground will be
If the time of flight i.e.time for reaching ground is taken to be T
then using the formula
dividing both sides by 4.9 we get
(negative time discarded)
So Hero's Horizontal displacement before reaching ground will be
Calculation of velocity at the time of reaching ground
Vertical component velocity at the time of reaching ground
Again horizontal component of the velocity at the time of reaching ground
So resultant velocity at the time of reaching ground
Direction of
Is it helpful ?


