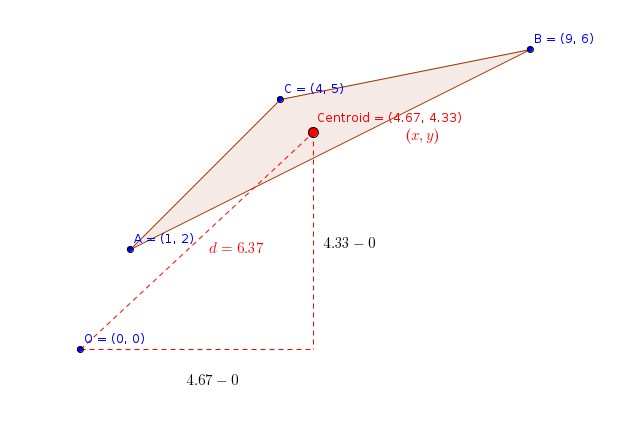
#"Strategy :"#
#diamond " find the centroid of triangle"#coordinates(x,y)
#diamond" find length between origin and centroid"#
#"The coordinates of Centroid "color(red)( Centroid(x,y))" can be calculated using :"#
#x=(x_1+x_2+x_3)/3#
#y=(y_1+y_2+y_3)/3#
#x=(1+9+4)/3=14/3=4.67#
#y=(2+6+5)/3=13/3=4.33#
#"The Centroid located :"color(red)(Centroid(4.67,4.33))#
#"............................................................................................"#
#"length between O(0,0) and "color(red)(Centroid(4.67,4.33))#
#d=sqrt((4.33-0)^2+(4.67-0)^2)#
#d=sqrt((4.33)^2+(4.67)^2)#
#d=6.37" units"#

