A triangle has corners at #(-4 ,2 )#, #(7 ,1 )#, and #(2 ,-7 )#. If the triangle is dilated by a factor of #2/5 # about point #(-1 ,4 ), how far will its centroid move?
1 Answer
the centroid will move by about
Explanation:
the solution:
the centroid of the given triangle is at
the reference point is at
Let the unknown new centroid be at
By segment division method
Also
The old centroid is at
The new centroid is at
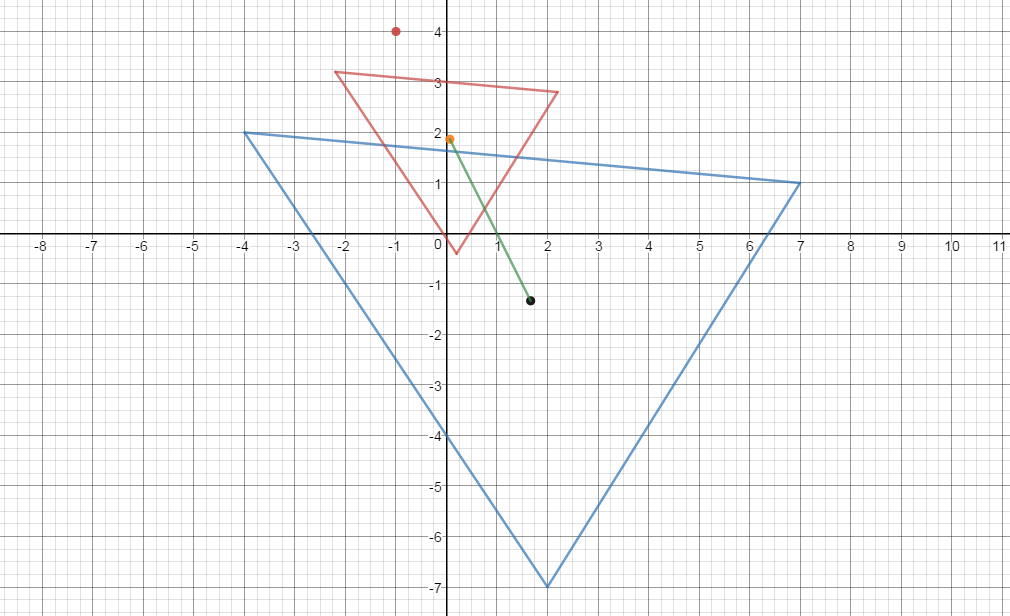
how far did the centroid move ?
God bless.... I hope the explanation is useful.
