Question

A triangle has corners at `(5 , 4 )`, ( 7, 1 )`, and`( 1, 3 )#. What are the endpoints and lengths of the triangle's perpendicular bisectors?

Answer 1

End points
`(51/14, 13/14), (6,5/2)`
`(51/14, 13/14), (3, 7/2)`
`(51/14, 13/14),(4,2)`

Explanation:

Perpendicular bisectors of a triangle, meet at a point. This point is the centre of the circumcircle of the triangle, and it is equidistant from the three vertices of the triangle. If this point is (x,y), then its distance from the points (5,4) , (7,1) and (1,3) would be

`sqrt((x-5)^2 +(y-4)^2)` , `sqrt((x-7)^2 +(y-1)^2)` and`sqrt((x-1)^2 +(y-3)^2)` . All these distances are equal and hence by equating any two pairs of distances, we can get two equations in x and y which can be solved to find x and y.

Thus, `sqrt((x-5)^2 +(y-4)^2)` = `sqrt((x-7)^2 +(y-1)^2)`,
Or,
`(x-5)^2 +(y-4)^2=(x-7)^2 +(y-1)^2`
This would give -10x+25-8y+16= -14x+49-2y+1

Or, 4x-6y=9. Similarly,
`sqrt((x-1)^2 +(y-3)^2)` =`sqrt((x-7)^2 +(y-1)^2)`
This would, on simplification as above, would give
-2x+1-6y+9= -14x+49-2y+1

Or 12x -4y=40 `->` 3x-y=10

Solving the two linear equations in x and y would give x=`51/14` and y=`13/14`

Thus one end point of all the perpendicular bisectors would be `(51/14, 13/14)`

The other end points would be the midpoints of the sides of the triangles. These would be
`((5+7)/2, (4+1)/2), ((5+1)/2, (4+3)/2), ((7+1)/2, (1+3)/2)`

Or (6, 5/2), (3, 7/2)and (4,2)

The length of the perpendicular bisectors can now be calculated using the distance formula.

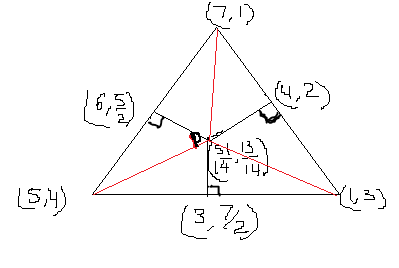
Length calculation would be a messy affair manually, hence skipped.