Question

A triangle has corners at `(5 ,7 )`, `(2 ,1 )`, and `(1 ,4 )`. What is the area of the triangle's circumscribed circle?

Answer 1

`color(blue)((25pi)/2" units"^2)`

Explanation:

The vertices of the triangle all lie on the circumference of the given circle. In order for us to find the area of the circle, we need to find its radius. There are different methods for doing this. We could use the equation of a circle and form a system of equations to find it, but another method is to know that the radius can be found using the sides and area of the triangle. It can be shown that:

`r=(abc)/(4*("Area of triangle"))`

I did the proof of this here:

https://socratic.org/questions/a-triangle-has-corners-at-9-7-2-5-and-5-4-what-is-the-area-of-the-triangle-s-cir#628258

Let:

`A=(5,7), B=(2,1), C=(1,4)`

Then using the distance formula:

`|AB|=|c|=sqrt((2-5)^2+(1-7)^2)=sqrt(45)=3sqrt(5)`

`|BC|=|a|=sqrt((1-2)^2+(4-1)^2)=sqrt(10)`

`|AC|=|b|=sqrt((1-5)^2+(4-7)^2)=sqrt(25)=5`

Area of `Delta ABC` using Heron' formula:

Heron's Formula:

`"Area"=sqrt(s(s-a)(s-b)(s-c))`

Where `a, b, c` are the lengths of the triangles sides and `bbs` is the semi-perimeter:

`s=(a+b+c)/2`

`s=(sqrt(10)+5+3sqrt(5))/2`

I will give you the results from the calculations, but won't do the steps. One of the big disadvantages to using area and sides of the triangle is the amount of work in finding these. Heron's formula will involve some time consuming arithmetic if the sides are in the form of surds, and the use of a computer to carry these out is a big advantage.

`"Area"=15/2`

`abc"=75sqrt(2)`

`"radius"=(abc)/(4("Area of triangle"))=(75sqrt(2))/(4(15/2))=(75sqrt(2))/30=(5sqrt(2))/2`

`"Area of circle"=pir^2=pi((5sqrt(2))/2)^2=(25pi)/2" units"^2`

PLOT:

Answer 2

`(5-2)^2+(7-1)^2= 45`
`(5-1)^2+(7-4)^2 = 25`
`(2-1)^2+(1-4)^2=10`

`pir^2 = {pi (45)(10)(25)}/{4(25)(10)-(45-25-10)^2} = { 25 pi}/2`

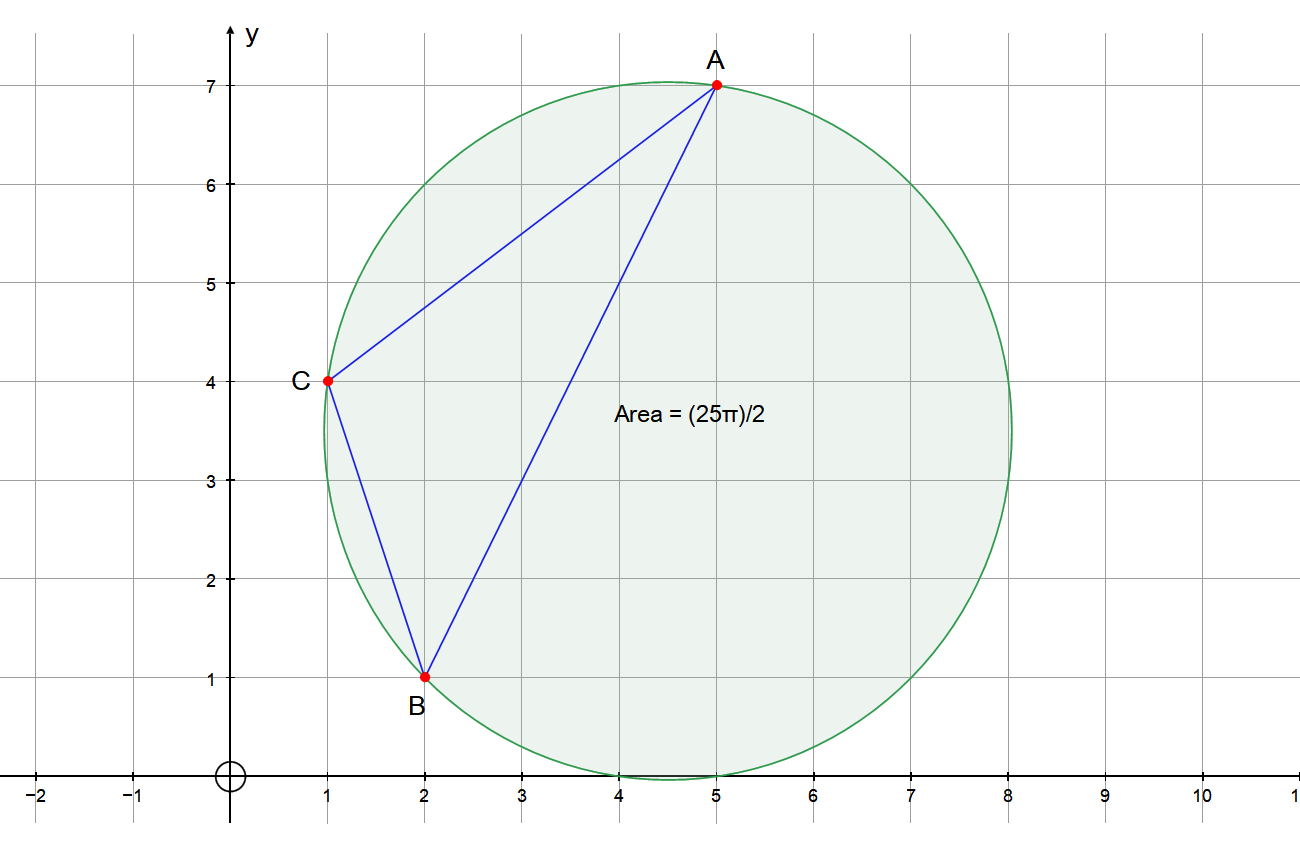
Explanation:

I'm really trying to teach Somebody Nice to do these so I don't have to answer them myself.

The radius of the circumcircle is the product of the triangle sides divided by four times the area. We're after `pir^2:`

`pir^2 = {pi a^2b^2c^2}/{16 (text{area})^2}`

There are many expressions for the area of a triangle. Given coordinates, the Shoelace Theorem is often best. Here we already need to calculate the squared sides for the numerator, so Archimedes' Theorem is indicated:

`16 (text{area})^2 = 4a^2b^2 - (c^2-a^2-b^2)^2`

All these exponents of two on the sides are just clutter. Let `A=a^2, B=b^2 and C=c^2` be the squared lengths of a triangle's sides.

`pir^2 = {pi A B C}/{4AB-(C-A-B)^2}`

We could just have started here. The points: `(5,7),(2,1), (1,4)`

`C=(5-2)^2+(7-1)^2= 45`

`B= (2-1)^2+(1-4)^2=10`

`A= (5-1)^2+(7-4)^2 = 25`

We're free to assign `A,B,C` however we like. I like making `C` the biggest.

`pir^2 = {pi (45)(10)(25)}/{4(25)(10)-(45-25-10)^2} = { 25 pi}/2`