Question

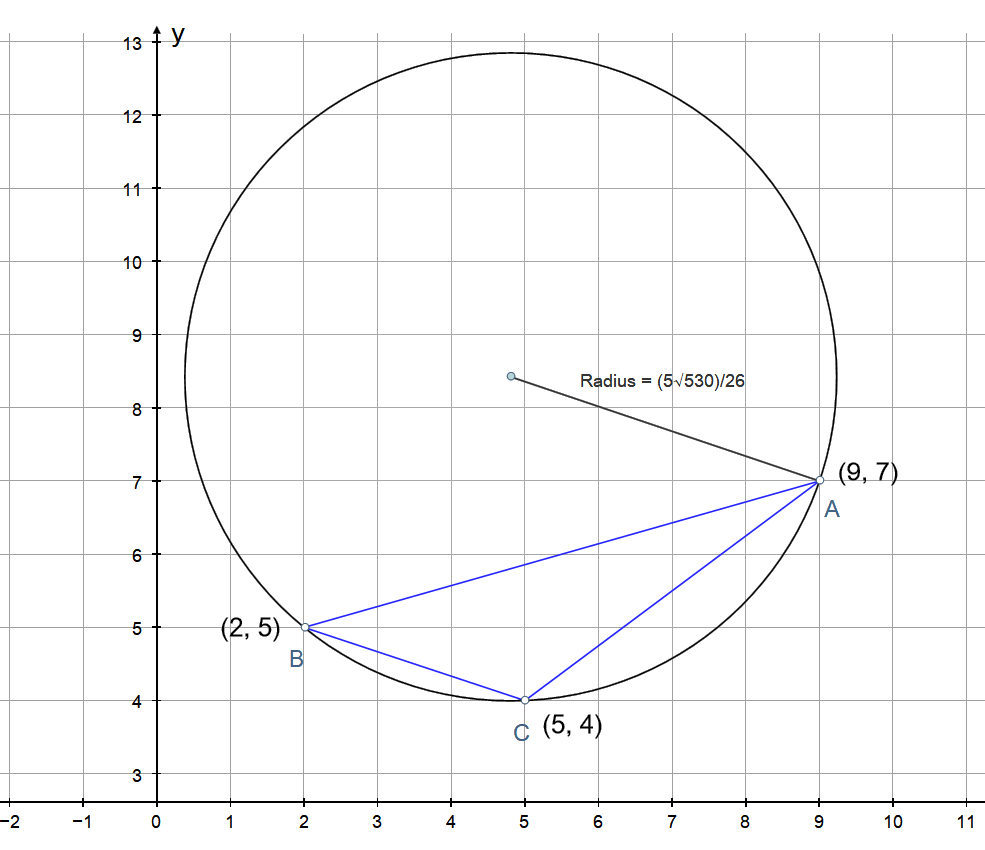
A triangle has corners at `(9 ,7 )`, `(2 ,5 )`, and `(5 ,4 )`. What is the area of the triangle's circumscribed circle?

Answer 1

`color(blue)("Area"=(6625pi)/338" units"^2`

Explanation:

In order to find the area of the circumscribed circle, we need to find the radius of this circle. It can be shown that:

`r=(abc)/(4("area of" Delta ABC))`

Where `a, b, c` are the sides of `Delta ABC`

We can prove this with the following:

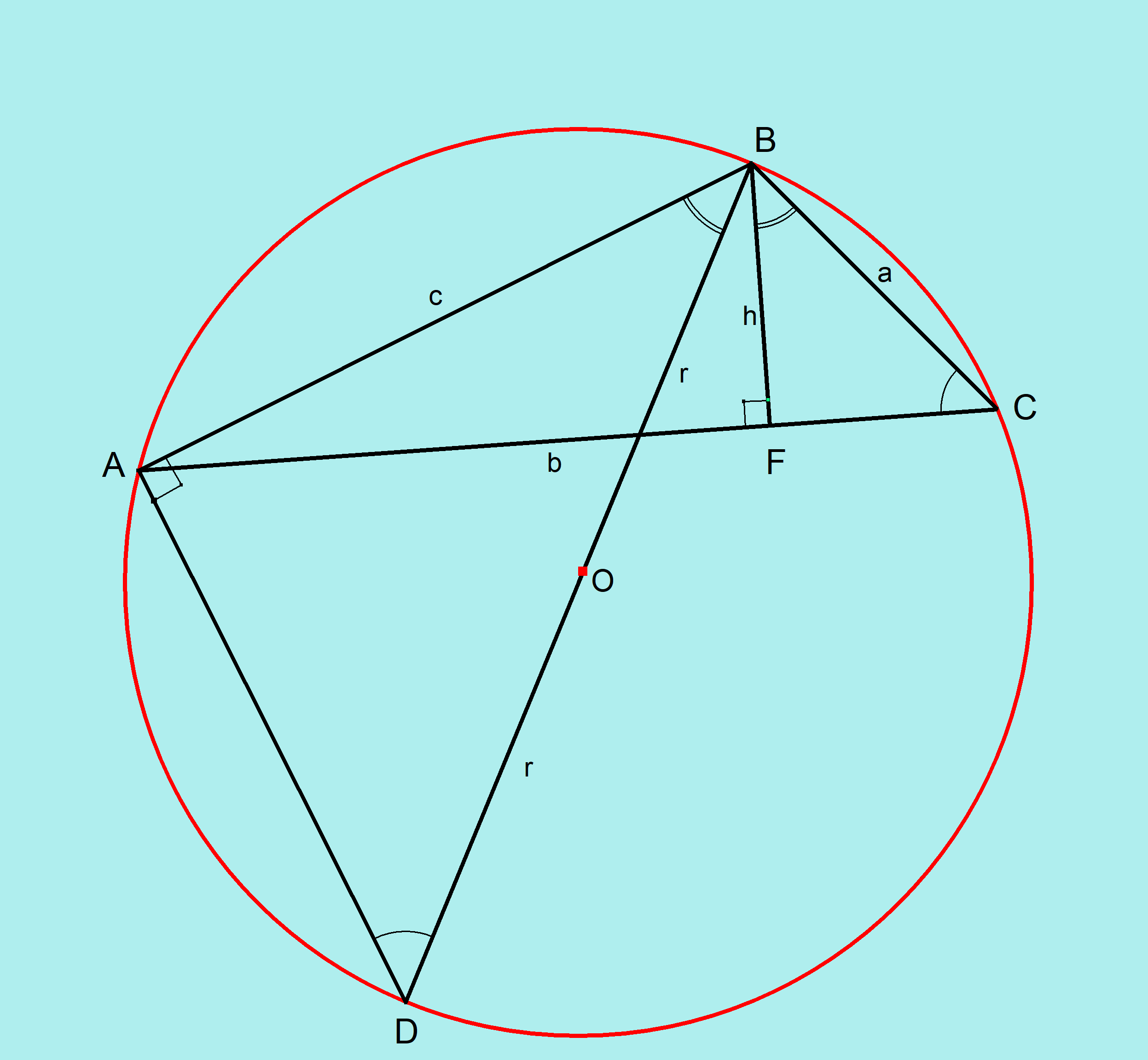
From diagram:

Draw a line from B to D through centre O. Notice that this is the diameter of the circle, and is twice the radius, so we can call this `2r`.

Let the altitude of `Delta ABC=h`

Then area of `DeltaABC=1/2bh`

`/_DAB=90^@`

The angle subtended at the circumference by the diameter is always a right angle.

`/_ADB=/_BCF`

These are angles subtended by the same chord AB

Looking at `DeltaABD` and `DeltaBCF` notice that:

`/_DAB=/_BCF` and `/_ADB=/_BCF` Therefore:

`DeltaABD` and `DeltaBCF` are similar. This means that:

`/_ABD=/_FBC`

Using the properties of similar triangles:

`c/(BD)=h/a`

`BD` is the diameter and so is equal to `2r`

`:.`

`c/(2r)=h/a \ \ \ \[1]`

`"Area of ABC"=1/2bh=>h=(2"Area of" ABC)/b`

Substituting this in `[1]`

`c/(2r)=(((2"Area of" ABC)/b))/a=(2"Area of"ABC)/(ab)`

After rearranging we have:

`r=(abc)/(4("Area of " ABC))`

Now we know the radius in terms of the sides and area of `ABC` we need to find these.

First the sides `a, b, c`, these can be found using the distance formula.

`|d|=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

Let the given points be:

`A=(9,7) , B=(2,5), C=(5,4)`

This gives sides:

`AB, BC, AC`

For `AB`

`|AB|=sqrt((2-9)^2+(5-7)^2)=color(blue)(sqrt(53)`

For `BC`

`|BC|=sqrt((5-2)^2+(4-5)^2)=color(blue)(sqrt(10)`

For `AC`

`|AC|=sqrt((5-9)^2+(4-7)^2)=sqrt(25)=color(blue)(5)`

Area of `DeltaABC`

Taking AC as the base, we now find the gradient of this line segment, then we find the equation of the line. We then find the equation of the line perpendicular to this passing through the vertex B.

Gradient of AC:

`m_1=(4-7)/(5-9)=3/4`

Using point slope form of a line and vertex `(5,4)`:

`y-4=3/4(x-5)`

`y=3/4x+1/4 \ \ \ \[2]`

A line perpendicular to this will have gradient:

`m_2=-1/m_1`

`m_2=-1/(3/4)=-4/3`

The line passes through `(2,5)`

Using point slope form of a line:

`y-5=-4/3(x-2)`

`y=-4/3x+23/3 \ \ \ \[3]`

The point of intersection of `[2]` and `[3]` will give us the co-ordinates of the base of the altitude through B.

Solving simultaneously:

`3/4x+1/4=-4/3x+23/3=>x=89/25`

Substituting in `[2]`

`y=3/4(89/25)+1/4=73/25`

Co-ordinates `(89/25,73/25)`

Let `D=(89/25,73/25)`

We now find the length of `DB` the altitude:

`|DB|=sqrt((2-89/25)^2+(5-73/25)^2)=sqrt(169/25)=13/5`

`"Area of " DeltaABC=1/2AC*DB`

`"Area of " DeltaABC=1/2(5)*(13/5)=13/2`

So:

`r=((sqrt(10))(5)sqrt(53))/(4(13/2))=((sqrt(10))(5)sqrt(53))/26=(5sqrt(530))/26`

Area of circumscribed circle is:

`"Area"=pi((5sqrt(530))/26)^2=(6625pi)/338" units"^2`

PLOT: